Nach meinem letzten Artikel zum Thema dWb+ ist bereits einige Zeit vergangen. Ich habe lange überlegt, wie ich eine Anwendung schreiben könnte, die mir gestattet, mit einem System herumzuspielen, das ich aus dem Buch von Prof.Strogatz kannte.

Das System zeigt, dass ein System, dessen Randbedingungen man modifiziert in einen anderen stabilen Fixpunkt wandern kann und dort auch verbleibt, wenn man die ursprüngliche Konfiguration wiederherstellt - um das System dazu zu bewegen, den initialen stabilen Fixpunkt wieder einzunehmen ist unter Umständen eine noch drastischere Änderung der Randbedingungen nötig. Die Beschreibung des Systems als Differentialgleichung lautet:

mit

und

Daraus ergibt sich

Mit den Werten m=-0.04 und n=0.45 ergibt sich für die drei Funktionen:

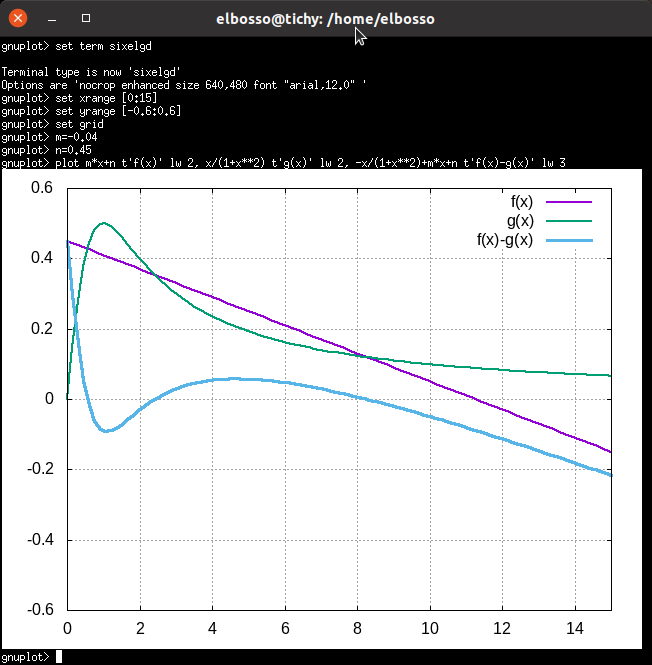Darstellung von f(x), g(x) und f(x)-g(x)

Man erkennt schnell die drei reellen Nullstellen - die befinden sich dort, wo sich f(x) und g(x) jeweils schneiden. Von links nach rechts handelt es sich dabei um einen stabilen Fixpunkt, gefolgt von einem instabilen und einem weiteren stabilen Fixpunkt. Diese Nullstellenanalyse ist wesentlich einfacher, als die Nullstellen des bestimmenden Polynoms

rechnerisch zu bestimmen - der Vollständigkeit halber: sie sind 0.5629613339656534 sowie 2.4161333991332405 und 8.270905266901107.

Das System hat zwei freie Parameter: m und n. Ändert man diese, verschiebt man in der Darstellung die Linie bzw. ändert ihre Steigung. Es ist klar, dass damit die Schnittpunkte mit g(x) und damit die Nullstellen und Fixpunkte des Systems ebenfalls verschoben werden und bei entsprechender Wahl der Parameter ganz verschwinden Das folgende Beispiel zeigt dies bei Wahl des Parameters n=0.57:

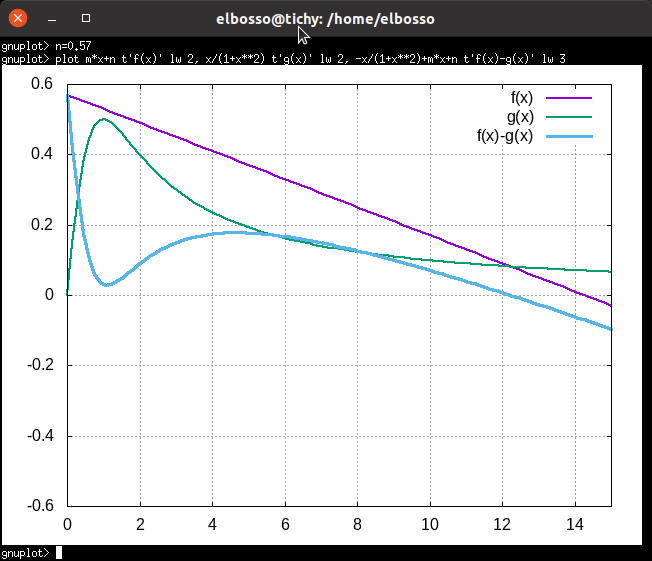Verschwinden der zwei linken Fixpunkte bei Änderung des Parameters n

Sorgt man dafür, dass die beiden linken Fixpunkte verschwinden, wird das System in den rechten hineinlaufen und wenn man die Änderungen nicht schnell genug rückgängig macht, befindet sich das System bereits auf der rechten Seite des instabilen Fixpunktes - man kann seine Entwicklung hin zum rechten Fixpunkt dann nicht mehr aufhalten.

Um das System davon zu überzeugen, wieder in den linken stabilen Fixpunkt zurückzukehren, muss man dafür sorgen, den rechten und den instabilen Fixpunkt verschwinden zu lassen - etwas, das nur durch drastische Überhöhung des Parameters m zu erreichen ist. Hier ist ein Beispiel dafür mit m=-0.06 dargestellt:

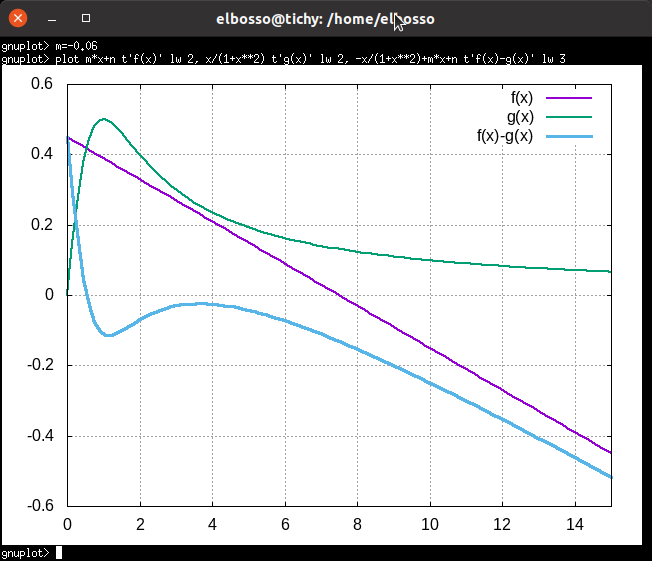Verschwinden der zwei rechten Fixpunkte bei Änderung des Parameters m

All das ist natürlich nicht annähernd so erhellend, wenn man diese Experimente nicht interaktiv druchführen und ein wenig mit den Parametern spielen kann. daher habe ich entsprechende Module in dWb+ geschaffen, mit denen man die Parameter der Systemgleichung (oder Funktion) interaktiv variieren und die Auswirkung auf die Entwicklung des Systems sofort studieren kann:

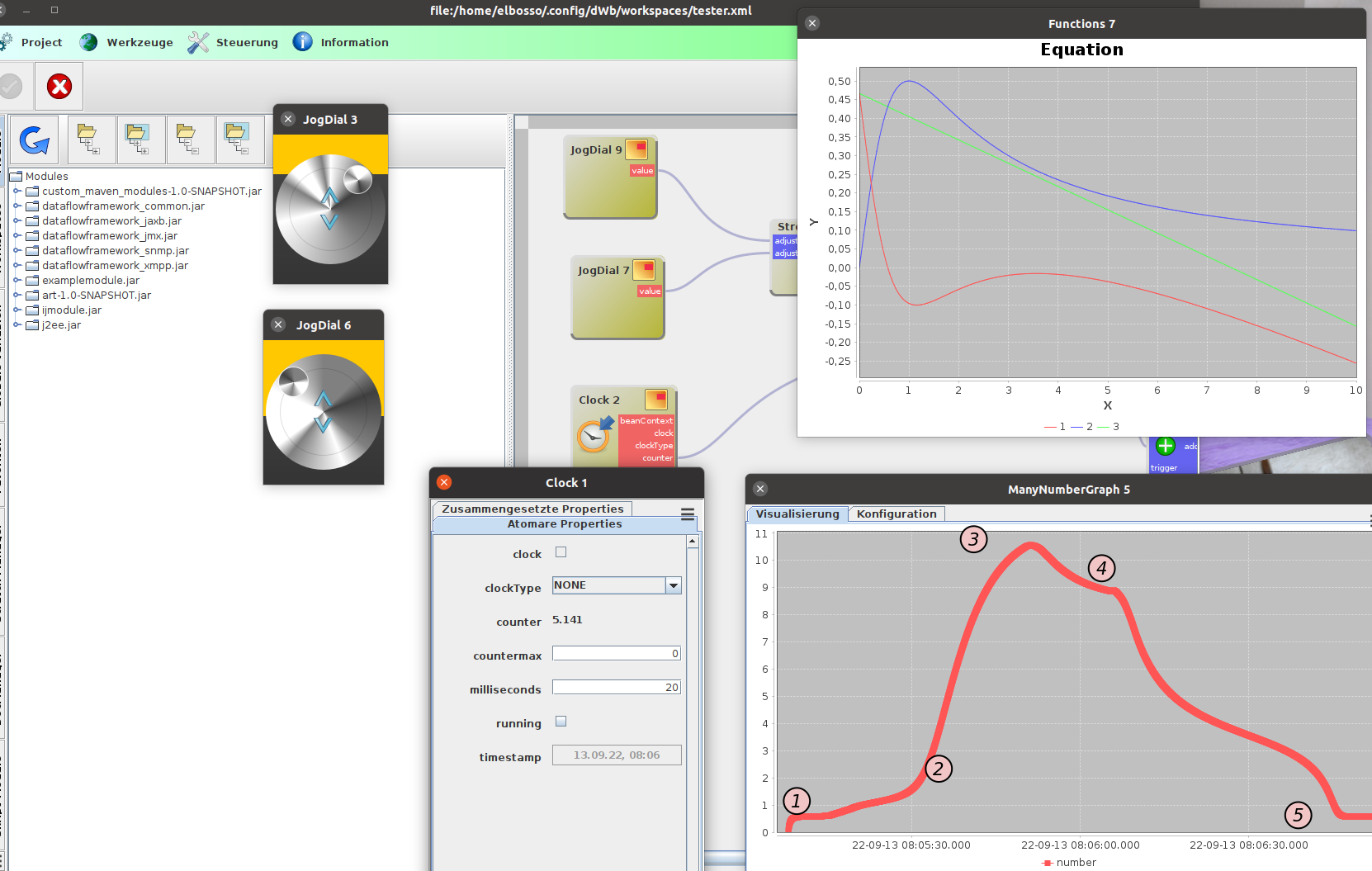Ein dWb+ Workspace zur interaktiven Exploration des Systemverhaltens

Man sieht die zwei Eingabeelemente zur Modifikation der Parameter m und n links, rechts oben sind die definierenden Funktionen dargestellt. Darunter findet man den Graph des Systemzustandes. Bei (1) befindet sich das System im linken Fixpunkt. Anschließend erfolgte eine Steigerung des Parameters n bis zum Verschwinden der beiden linken Fixpunkte, das gleichzeitig den rechten Fixpunkt bis jenseits der 10 verschob und dafür sorgte, dass sich das System in Richtung dieses Fixpunktes bewegte (2), den es schließlich auch erreichte (3). Anschließend wurde der Parameter n wieder auf den initialen Wert zurückgesetzt, was aber wie beschrieben dafür sorgte, dass das System im rechten Fixpunkt (4) hängenblieb. Erst die Erhöhung des Parameters m sorgte dann dafür, dass die beiden rechten Fixpunkte verschwanden und das System sich wieder in den ursprünglichen zurückbewegen (5) konnte.

Artikel, die hierher verlinken