Ich habe mich längere Zeit nicht mehr mit den Themen Chaos und nichtlineare Systeme beschäftigt - Zeit, das nachzuholen...

Das elastische Pendel wird durch die folgenden Differentialgleichungen zweiter Ordnung beschrieben:

Mit

können wir diese in vier Differentialgleichungen erster Ordnung dekomponieren, die sich dann einfach numerisch behandeln lassen:

Stellt man nun die Länge des Pendels und dessen Winkel graphisch dar, erhält man für die Parameter

und die Anfangszustände

folgende Trajektorie (die Berechnung erfolgte bis t=84 Sekunden):

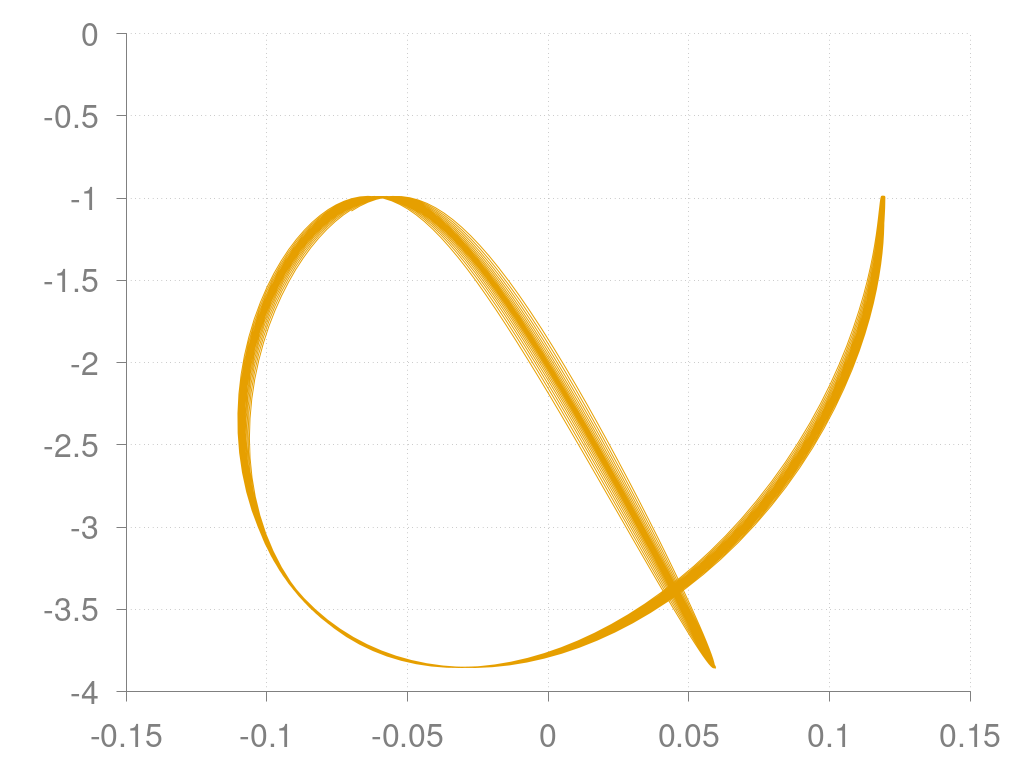Position des Masseschwerpunkts des Pendels

Dabei beginnt das Pendel zunächst damit, sich zu verlängern. Kurz nach Durechlaufen des Tiefstpunktes verkürzt sich das Pendel wieder, um in der Nähe des linkenUmkehrpunktes seine kürzeste Länge zu erreichen und wieder mit der Expansion zu beginnen. Man sieht bereits hier, dass dieser Vorgang sich nicht periodisch wiederholt - die Rajektorie wiederholt sich nicht exakt, sondern verschmiert.

Trägt man nur den Winkel über die Zeit auf, sieht der Verlauf wie folgt aus:

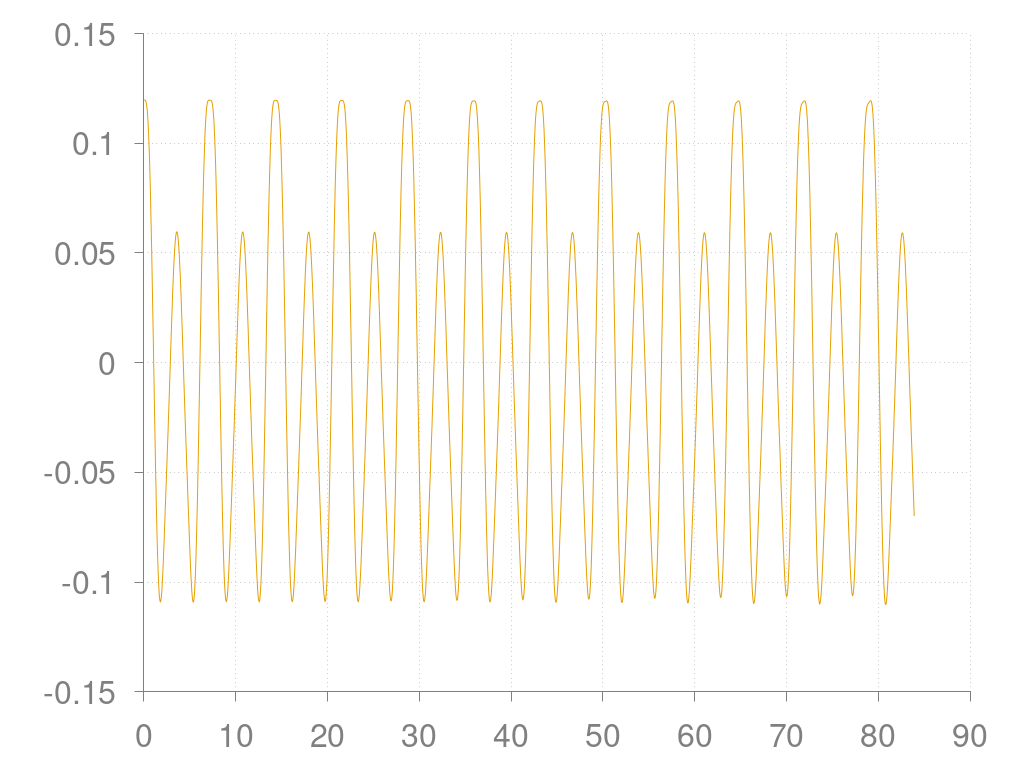Verlauf des Pendelwinkels über die Zeit

Hier ist man noch leichter geneigt, zu glauben, dass man ein System mit einem periodischen Verlauf vor sich hat. Lässt man die Simulation weiter laufen, zeigt sich aber schnell, dass dem nicht so ist - hier die Trajektorie und der Winkel über der Zeit für den Bereich zwischen t=168 s und t=252 s:

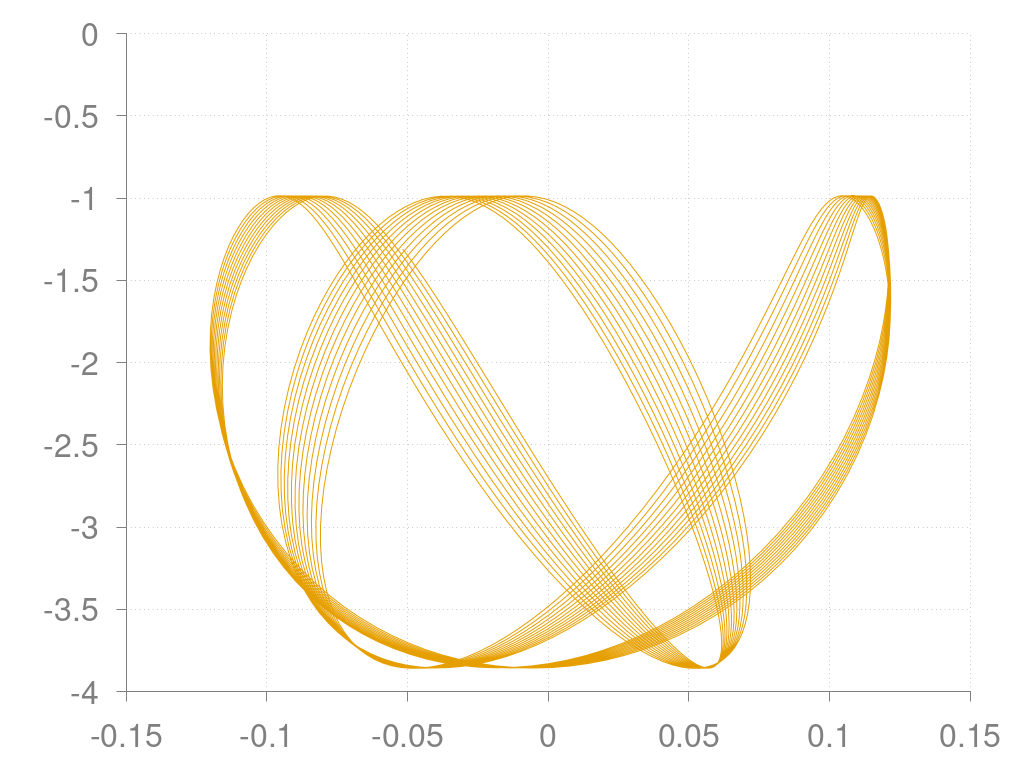Position des Masseschwerpunkts des Pendels

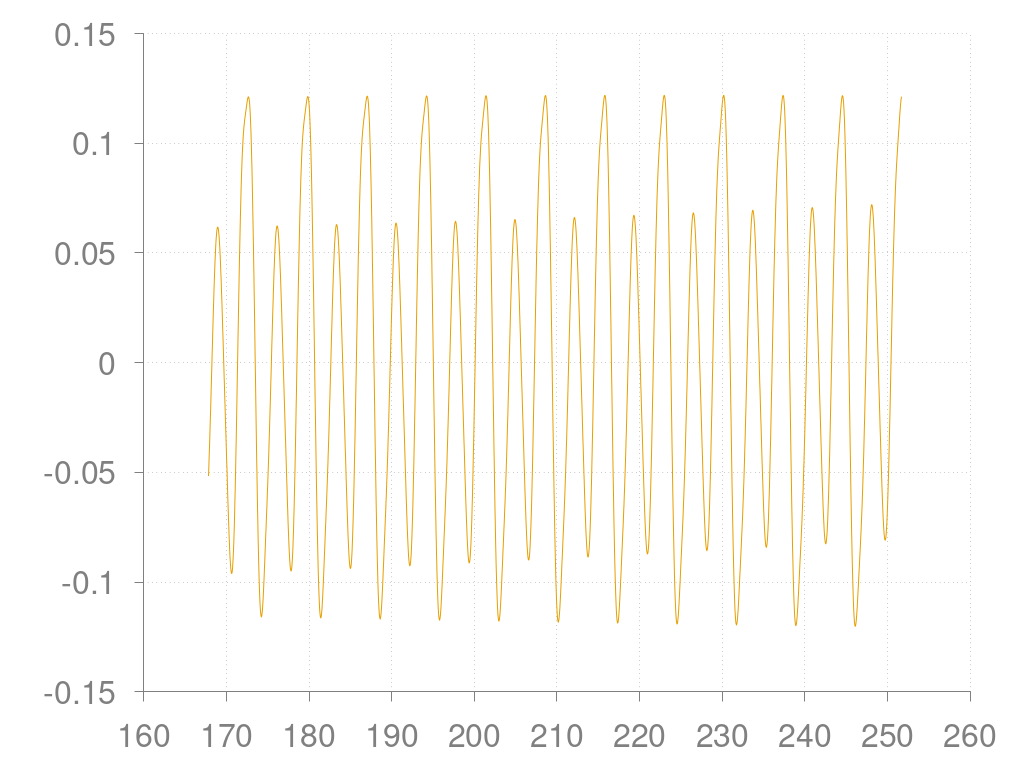Verlauf des Pendelwinkels über die Zeit

Und hier noch einmal zur Veranschaulichung die Entwicklung der Trajektorie bis zu t=1400 s, wobei zur besseren Veranschaulichung die Bewegung in der Zeit auf eine dritte Achse abgetragen und die Trajektorie abhängig vom Zeitpunkt eingefärbt wurde:

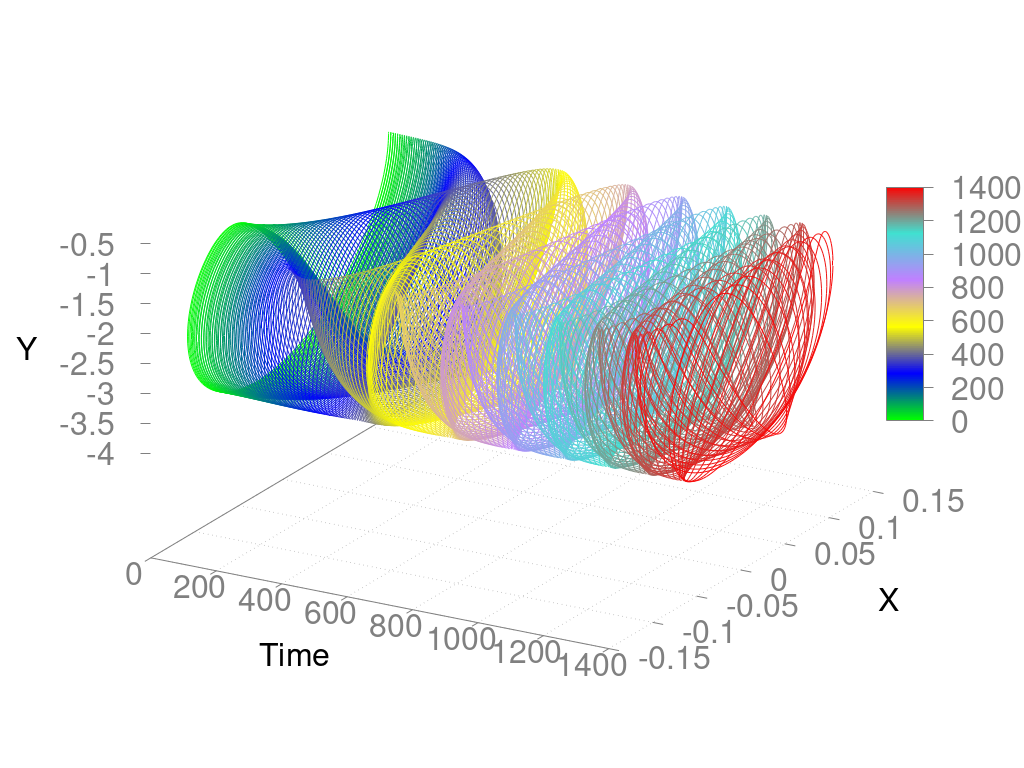Position des Masseschwerpunktes über die Zeit