Updates

• 19. Januar 2025

Nachdem wieder einige Zeit vergangen ist, seit ich mich mit den Themen Chaos und nichtlineare Systeme beschäftigt habe, habe ich nun ein neues, mir bisher unbekanntes System gefunden, mit dem ich ein wenig experimentieren wollte

Das CORD System wird durch die folgenden Gleichungen beschrieben:

Mit den im oben verlinkten Artikeln angegebenen Parametern

ergibt sich der Strange Attractor im Zustandsraum, der sich wie folgt darstellt:

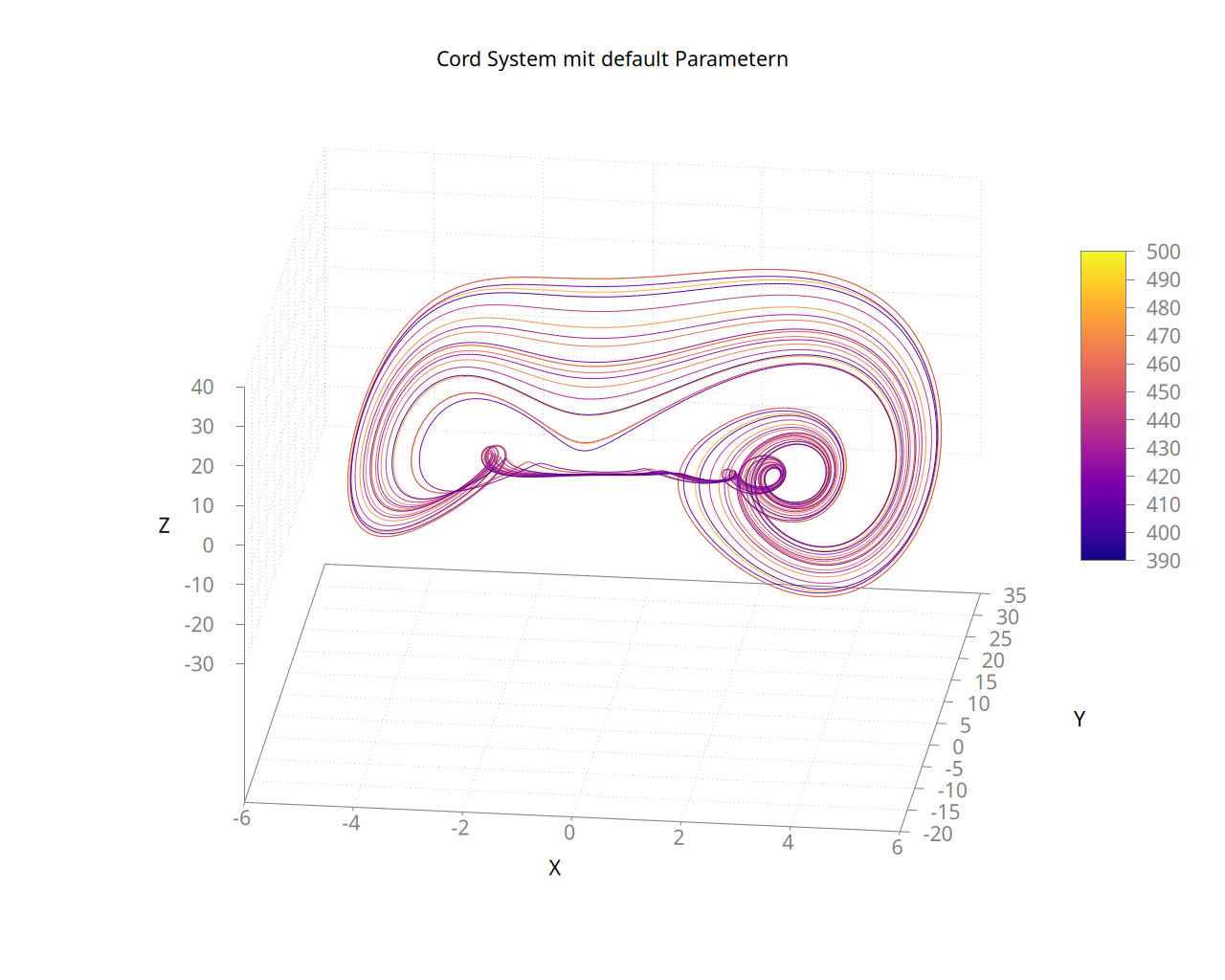Darstellung des Systems mit den aus diversen Veröffentlichungen bekannten Standardparameterwerten

Diese Gestalt des Attractor ist für das System wohlbekannt. Auch die Untersuchung nach dem Parameter b ist allgemein bekannt - man findet bei Varation dieses PArameters diverse chaotische Regionen genau wie Periodenverdoppelung. Ich habe mich also anderen Experimenten zugewandt: Variationen der Parameter F und a.

Variiert man den Parameter F, findet man zunächst, dass sich auch hier chaotische Regionen und periodische finden lassen: Die folgende Abbildung zeigt etwa bei den Werten 7 und 12 ein periodisches Verhalten, während der Wert 10 zu einer Konfiguration mit vierfacher Periode führt. Die Werte 6 und 12 hingegen zeigen einen charakteristischen Strange Attractor - wobei man sehen kann, dass der Wert des Parameters scheinbar die Ausdehnung des Attractor bestimmt - das kann man sich bei genauerer Betrachtung der Gleichungen auch intuitiv erklären.

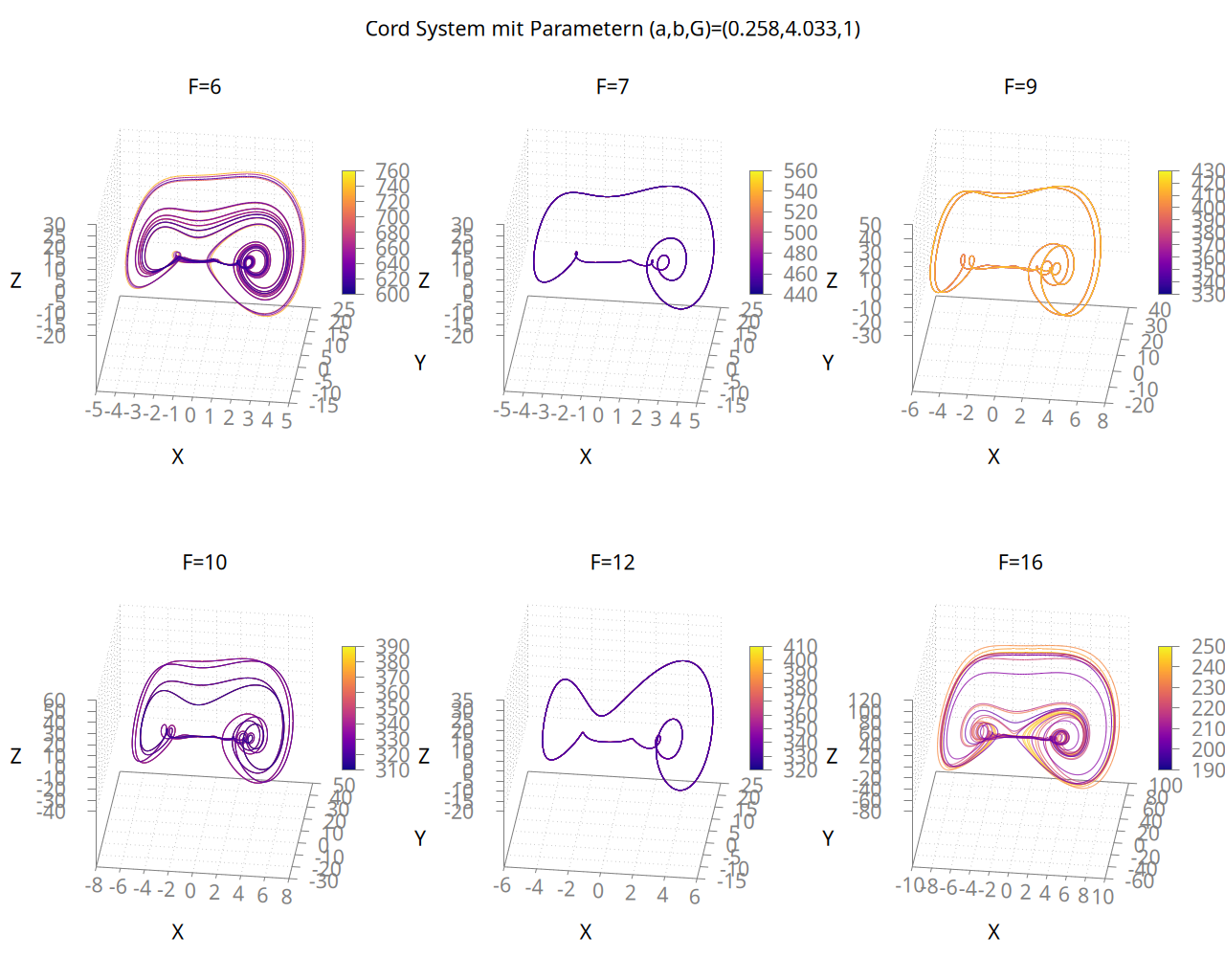Darstellung des Systems mit den aus diversen Veröffentlichungen bekannten Standardparameterwerten unter Variation von F

Die Variation des Parameters A war aus meiner Sicht noch interessanter: Der bekannte Strange Attractor, der sich aus den Standardwerten der Parameter ergibt besteht ja eigentlich aus drei Rollen: eine im negativen X-Bereich, eine im positiven X-Bereich, die beide durch einen Schlauch verbunden sind un eine große, die den Kreis dann wieder schließt. Schaut man sich nun das Verhalten des Systems bei verschiedenen Werten von a an, sieht man überaschenderweise, dass eine der beiden kleinen Rollen verschwindet: Bei einem Wert von 0.4 ist noch ein Rest der kleinen Rolle im negativen X-Bereich zu erkennen, bereits bei einem Wert von 0.5 verschwindet sie komplett. Auch bei einem Wert von 0,6 bleibt sie verschwunden, allerdings ist dann auch wieder ein periodisches Verhalten (doppelte Periode) des Systems zu beobachten. bei einem Wert von 0.8 sind wir wieder im chaotischen Regime angekommen - jedoch fehlt die Rolle weiterhin. Der Wert 1.1 zeigt eine weitere Periodenverdopplung, während das System mit einem Wert von 1.2 für a wieder einen Strange Attractor ausbildet, der aber weiterhin die Rolle bei negativen Werten für X vermissen lässt.

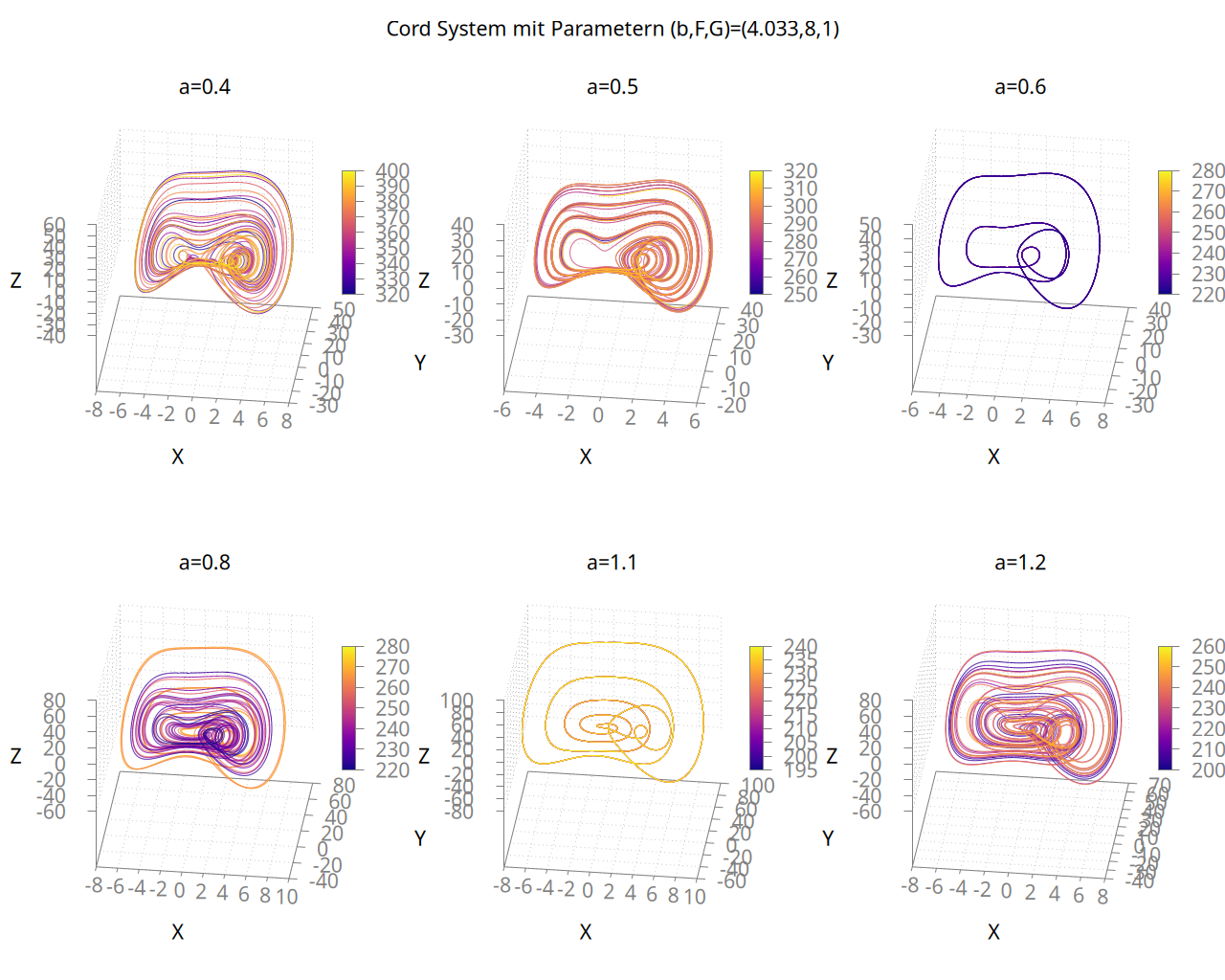Darstellung des Systems mit den aus diversen Veröffentlichungen bekannten Standardparameterwerten unter Variation von a

Aktualisierung vom 19. Januar 2025