Ich wollte als Vorbereitung eines neuen Projektes im Dunstkreis computergenerierter "Kunst" die Simulation von Körpern in einem Gravitationsfeld simulieren.

Ich habe vor geraumer Zeit bereits einmal einen Spezialfall des 3-Körper-Problems implementiert und analysiert.

Nachdem ich neulich die Worley-Noise Funktion implementiert habe, habe ich überlegt, wie die Visualisierung dieser Funktion aussähe, wenn ich die Stützstellen als massebehaftete Körper betrachtete und die Bewegung im resultierenden (zweidimensionalen) Schwerefeld simulieren würde.

Dazu benötigte ich zunächst ein entsprechendes Differentialgleichungssystem, das ich dann mit meinen numerischen Lösungsverfahren iterieren kann.

Ich schreibe dieses Mal bewusst nicht die entsprechenden Formeln auf - die lassen sich leicht im Internet finden. Ich präsentiere hier lediglich den Schritt des numerischen Verfahrens, der aus den Zuständen des vorhergehenden Iterationsschritts die Zustandsänderung des aktuellen Iterationsschritts berechnet:

public double[] calculateDerivatives(double[] states)
{
	if(states.length/4!=masses.length)
		throw new java.lang.IllegalArgumentException("number of states and number of masses must match!");
	double[] rv=new double[states.length];

	for(int i=0;i<masses.length;++i)
	{
		double forcex=0;
		double forcey=0;
		double vx=states[i*4];
		double sx=states[i*4+1];
		double vy=states[i*4+2];
		double sy=states[i*4+3];
		for(int j=0;j< masses.length;++j)
		{
			if(j!=i)
			{
				double xdist=sx-states[j*4+1];
				double ydist=sy-states[j*4+3];
				double distance=java.lang.Math.sqrt(xdist*xdist+ydist*ydist);
				forcex-=masses[j]*xdist/distance;
				forcey-=masses[j]*ydist/distance;
			}
		}
		double vxpunkt = forcex;
		double sxpunkt=vx;
		double vypunkt = forcey;
		double sypunkt=vy;
		rv[i*4+0] = vxpunkt;
		rv[i*4+1] = sxpunkt;
		rv[i*4+2] = vypunkt;
		rv[i*4+3] = sypunkt;
	}
	return rv;
}

Mein erster Versuch war bereits vielversprechend: Mit 4 Körpern ergeben sich daraus 16 gekoppelte Differentialgleichungen, die ich mittels des Runge-Kutta-Fehlberg-Solvers behandelte. Die vier Körper hatten eine identische Masse und unterschiedliche Startpositionen, die Geschwindigkeitskomponenten zum Zeitpunkt t=0 waren allesamt 0 - lediglich einer der Körper hatte eine Geschwindigkeitskomponente in y-Richtung mit dem Betrag 3. Die Entwicklung der Positionen der vier Körper kann man in den folgenden Abbildungen betrachten - der einzige Unterschied in den Anfangszuständen ist das Vorzeichen der Geschwindigkeitskomponente mit Betrag 3:

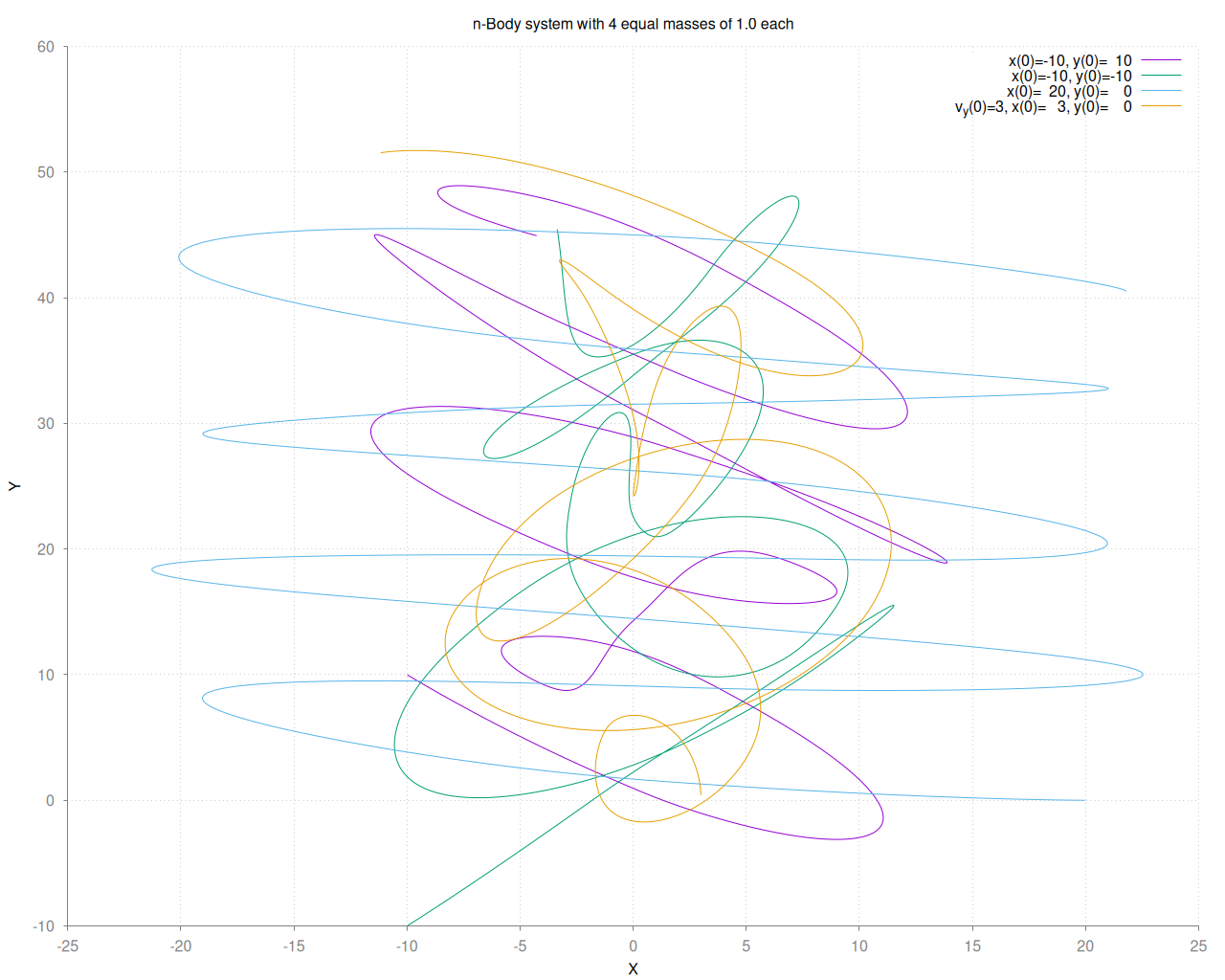Entwicklung des Systems mit Startgeschwindigkeit +3

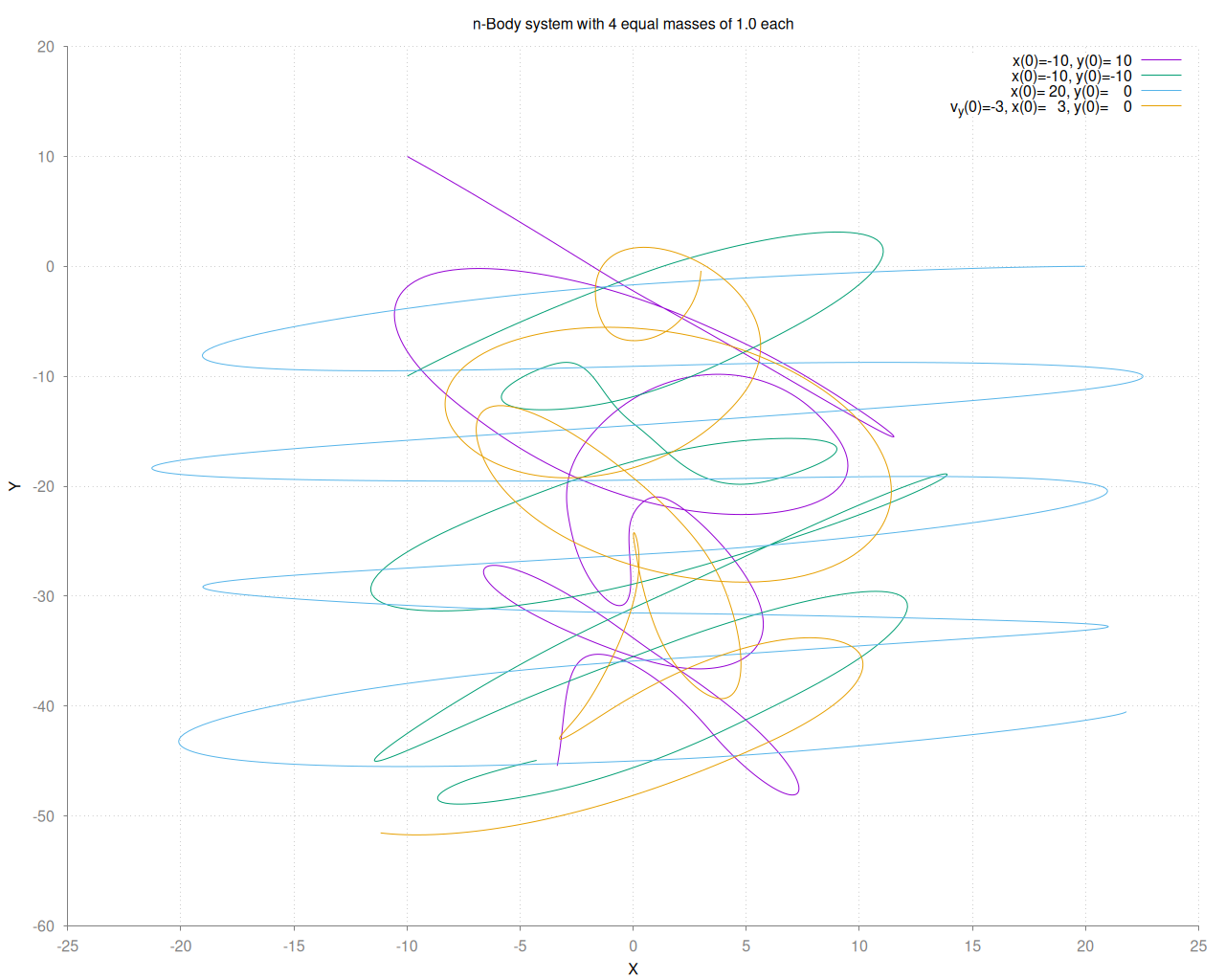Entwicklung des Systems mit Startgeschwindigkeit -3