Ich habe in einem vorhergehenden Artikel ein Paper zur Synchronisierung chaotischer Systeme nachvollzogen. Dort hatte ich gezeigt, dass - anders als im ursprünglichen Paper - eine Synchronisierung zweier gleich parametrierter Lorenz-Systeme bei geeigneter Parameterwahl auch über die Zustandsvariable z möglich ist.

Ich wollte nun herausbekommen, ob ich die Synchronisierung wieder aushebeln könnte, wenn ich einen anderen der drei Parameter variiere - über z konnte ich die Systeme ja durch die Anpassung des Parameters beta synchronisieren, was beim klassischen Parametersatz für das Lorenz-System ja nicht gelungen war. Die Frage stellte sich also, ob ich mit dem dort herausgefundenen Parameterwert für beta die anderen beiden Parameter so ändern könnte, dass die Synchronisierung nicht mehr über alle drei Zustandsvariablen funktioniert.

Ich schiebe hier noch eine kurze Bemerkung zum Thema Chaos ganz allgemein ein: Mancher hat als eine Definition des Chaos gehört, dass initial beliebig nahe Trajektorien sich über die Zeit exponentiell voneinander entfernen und nun wird gezeigt, dass man Trajektorien nicht nur dazu bringen kann, sich einander anzunähern, sondern sogar dazu, identische Werte anzunehmen. Dies steht nicht im Widerspruch zur Definition des Chaos, denn die vollständige Definition umfasst außerdem den Term unabhängig voneinander. Die Kopplung hebt aber gerade diese unabhängigkeit auf, da ja in jedem Schritt die Trajektorie korrigiert wird.

Nun zurück zum Thema: Der Parametersatz, der im letzten Artikel zum Thema dazu führte, dass die zwei Systeme sich über alle drei Zustandsvariablem synchronisieren ließen war ja

Durch die Berechnung des Bifurcationsdiagramms kann man Bereiche für Parameter ermitteln, in denen das System chaotisches Verhalten, bzw. einen seltsamen Attraktor aufweist. Für das Lorenz-System mit den angegebenen Parametern ist das Diagramm für Variation von rho hier dargestellt:

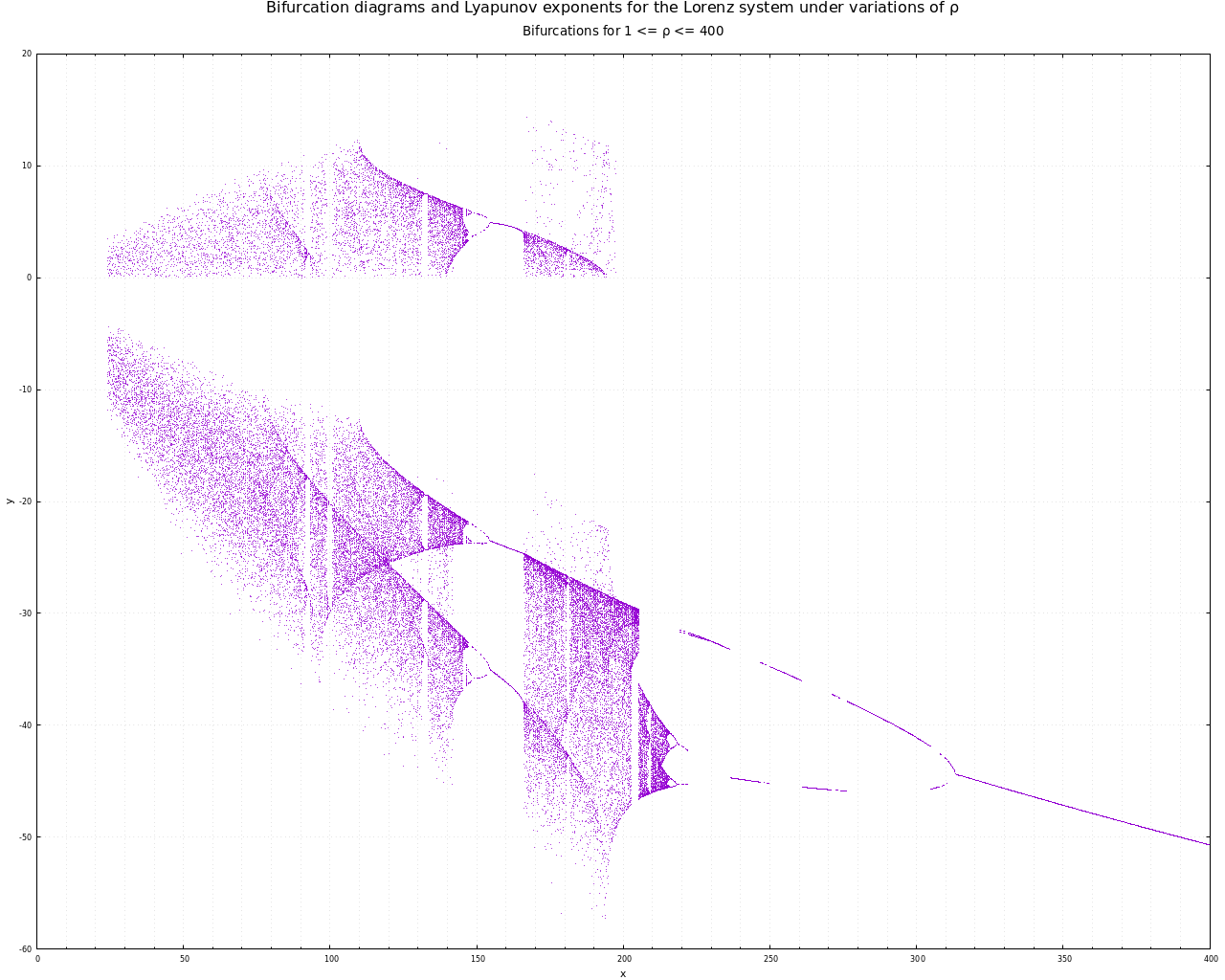Bifurkationsdiagramm für das Lorenz-System unter Variation des Parameters rho

Man erkennt wechselnde Bereiche mit klarer Periodizität und chaotischem Verhalten. Ich wählte einige Parameter aus den Abschnitten mit chaotischem Verhalten und versuchte, entsprechend parametrierte Systeme zu synchronisieren. Der erste Versuch erfolgte mit dieser Parametrierung:

Daraus ergab sich das bekannte Verhalten: Synchronisierung gelang über zwei der drei Zustandsvariablen. Das Ergebnis für z ist hier abgebildet:

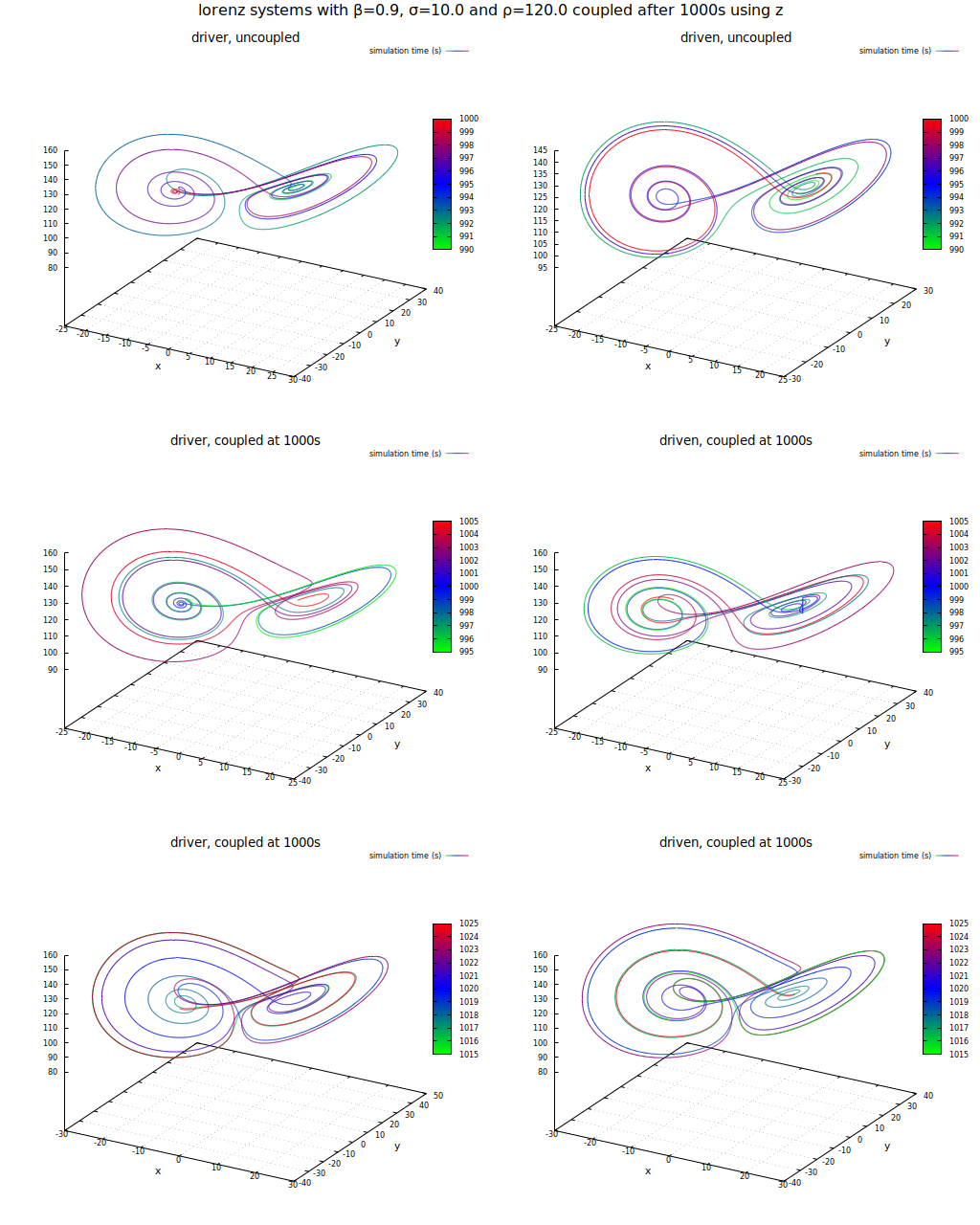Trajektorien nach Synchronisierung über z bei rho=120

Alle meine Versuche, einen weiteren Wert von rho im Bifurkationsdiagramm zu finden, für den das System über z synchronisierbar wäre schlugen fehl. Als ein Beispiel soll hier das Ergebnis für folgenden Parametersatz dienen:

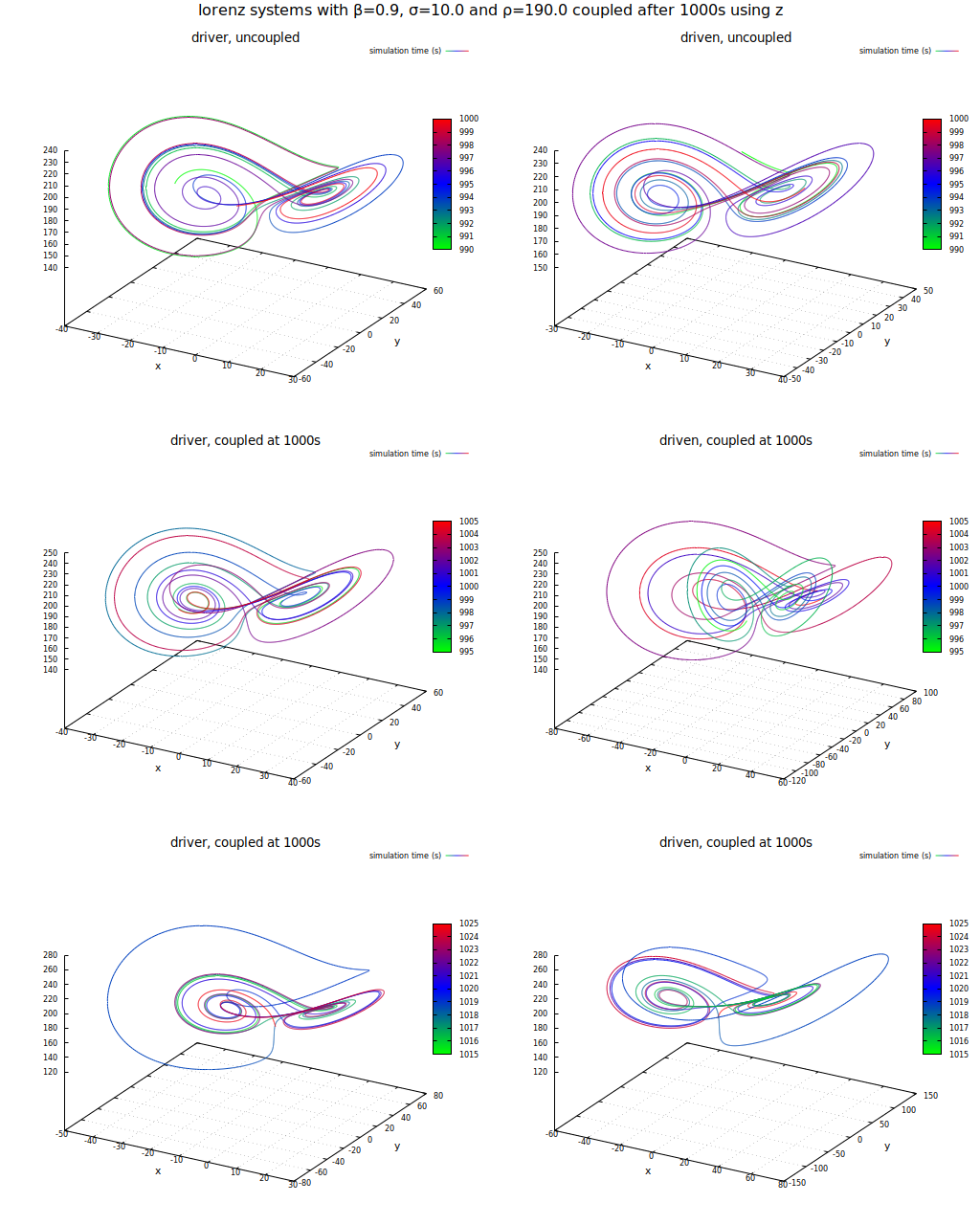Trajektorien nach Synchronisierung über z bei rho=120

Damit muss man aber die ursprüngliche Idee der Synchronisierung chaotischer Systeme - zumindest für das Lorenz-System - in Frage stellen: Die Idee war ja, dies als Übertragungsmedium vertraulicher Botschaften nutzen zu können, indem man die Botschaft auf eine der Zustandsgrößen aufprägt und der Empfänger durch die Synchronisierung auf das übertragene Signal die Originalbotschaft wieder herausrechnen kann. Teil des geheimen Schlüssels sind die Parameter des Systems. Durch die Tatsache, dass die Synchronisierung nur in einem Teilbereich des Parameterraums funktioniert, reduziert sich der Schlüsselraum erheblich. Aus Sicht der Kryptoanalyse stellt das einen Schwachpunkt eines solchen Verfahrens dar. Man darf dies natürlich nicht verallgemeinern - es kann durchaus sein, dass Systeme existieren, die über den gesamten Parameter-Raum hinweg synchronisierbar sind.

Artikel, die hierher verlinken