Angeregt durch einen Artikel auf Arxiv im letzten Jahr recherchierte ich ein wenig und stieß auf viele Diskussionen von Kuramoto Oszillatoren im Internet - so viele, dass ich auch damit experimentieren wollte.

Dieser Artikel ist zwar unter Chaos eingereiht - treffender müsste man ihn allerdings unter "Emergenz" oder "Selbstorganisation" fassen. Bei meinen Versuchen stellte sich heraus, dass man mit den richtigen Parametern nicht nur die ursprüngliche Art der Synchronisierung erreichen kann - näheres dazu weiter unten...

Ich begann mit dem ursprünglichen Standard-Modell

Dieses Modell beschreibt die Phasenänderung eines jeden Oszillators abhängig von seiner Eigenfrequenz und der durch die Kopplungskonstante modulierten Einflüsse aller anderen Oszillatoren im System.

Anschließend modifizierte ich die Gleichung so, dass die Einflüsse der anderen Oszillatoren nur noch regional und nicht mehr global wirksam wurden:

Dabei ist zu beachten, dass die eindimensionale Anordung von Oszillatoren als Ring verstanden wird - sonst würden auf die Oszillatoren am rechten und linken Rand weniger Einflüsse von ihren Nachbarn wirken.

Diese "Box"-Nachbarschaft variierte ich anschließend noch ein wenig wie folgt:

Wobei galt:

Und die Gewichte selber durch entsprechende Funktionen über den Abstand der beiden Oszillatoren i und j bestimmt wurden - wieder wurde hier von der Topologie eines Rings für die Kopplung der Oszillatoren ausgegangen.

Als Funktionen für die Gewichte wurden die (vereinfachte) Gauss-Verteilung

und das Ricker-Wavelet betrachtet:

Dabei ist wieder zu beachten, dass im Argument der Funktionen der Abstand der beiden Oszillatoren auf dem Ring gemeint ist.

Für diese Untersuchungen wurde die Erstellung einer GUI nötig, mit der ich die Parameter der Gewichtsfunktionen, die Gewichtsfunktion selbst und den Kopplungsfaktor variieren und den Einfluss auf die Phasen der Oszillatoren beobachten konnte. Für den eindimensionalen Fall sah ein erster Entwurf der GUI wie folgt aus:

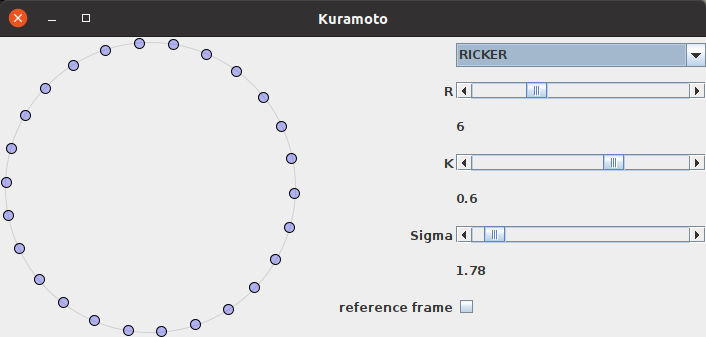GUI für die Experimente mit Kuramoto-Oszillatoren in einem eindimensionalen Ring

Interessant fand ich bei diesen Experimenten die Tatsache, dass es bei der Benutzung der Formel des Ricker-Wavelets für die Bestimmung der Gewichte mit denen benachbarte Oszillatoren einander beeinflussten Werte für dessen Parameter gab, bei dem die Phasen sich nicht synchronisierten, sondern sich (nahezu) äquidistant verteilten - wurde dieser Parameterbereich verlassen, stellte sich wieder die Synchronisation ein - egal, ob der Bereich nach unten oder oben verlassen wurde! Ein Beispiel für eine solche Verteilung der Phasen über den gesamten zur Verfügung stehenden Bereich ist in der obigen Abbildung dargestellt. Dabei war die Stärke des Kopplungsfaktors nahezu unerheblich - bei sehr kleinen Werten dieses Parameters wurde die Kopplung der benachbarten Oszillatoren natürlich unwirksam und damit folgte jeder wieder seiner Eigenfrequenz - allerdings stellte sich die äquidistante Verteilung bereits bei geringer Stärke der Kopplung ein und bleib von da an stabil. Diesseits und jenseits des für die äquidistante Verteilung der Phasen benötigten Wertes für Sigma wirkte sich eine Änderung der Kopplungskonstanten durchaus aus: Je höher deren Wert, desto geringer die Varianz der Phasen zwischen den einzelnen Oszillatoren.

Artikel, die hierher verlinken