Generator für beliebige TeX-Formeln

vorhergehende Artikel in: Java

03.04.2021

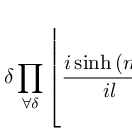
Meine Funde neulich auf dem Arxiv-Preprint-Server haben mich auf folgende Idee gebracht: Es gab in der Vergangenheit diverse Papers, die komplett durch eine sogenannte "AI" erstellt wurden und es trotz der Tatsache, dass sie keinen einzigen sinnvolen Gedanken enthielten durch den Peer-review-Prozess geschafft haben und veröffentlich wurden. Das betrifft aber nur Text - was, wenn man in einem solchen generierten Produkt auch einige kompliziert aussehenden Formeln benötigt?

Nun - der Ausgangspunkt war natürlich eine gründliche Internet-Recherche: So etwas schien es wirklich noch nicht zu geben. Also setzte ich mich hin und erstellte - die Arbeit ging wirklich gut von der Hand - in unter zwei Stunden die Version 1.0 dieser Lösung.

Momentan erstellt sie lediglich den TeX-Quelltext für die Gleichung und aktuell auch nur eine isolierte Gleichung. Aber dafür kommen beinahe beliebig komplex wirkende Konstrukte heraus, die bei flüchtigem Hinsehen tatsächlich als mathematische Gleichungen durchgehen können.

Der Quelltext kann für eigene Experimenmte in einen der zahlreichen Online-TeX-Compiler eingegeben werden...

Hier einige Beispiele:

i=\delta \prod\limits_{\forall \delta }\left\lfloor \frac{i\sinh \left(m_{l}\right)}{il}+am\cos \left(x\right)-m\gamma -y\omega \sum\limits_{m=\epsilon }^{k}\left\lceil \sigma \right\rceil \alpha \sin \left(z\lg \left(x_{\delta }\right)\alpha x\right)\beta \ln \left(\sqrt{\omega \sinh \left(x^{l}\right)}\right)-x\tan \left(y\delta _{\sigma }*\epsilon \sigma ^{j}-\epsilon \alpha \delta +\theta \beta \right)*a\frac{y\prod\limits_{z=m}^{\infty }\left\| ya_{i}\omega j^{\alpha }\right\| }{j\sigma }\right\rfloor

\omega =\beta lk\gamma \alpha y-xc\sigma ji-\beta \prod\limits_{j=l}^{\infty }\left\lceil \theta c*\gamma y_{x}\right\rceil cjj*y\omega _{z}

i=\theta cc-\delta \int\limits_{\gamma =i}^{\infty}\left\langle \alpha ^{4}\right\rangle

\beta ^{2}\simeq j\sum\limits_{\forall \epsilon }\left\langle mx*j\prod\limits_{l=\sigma }^{c}\left\lceil x\right\rceil \right\rangle

\omega _{1}=k\frac{jl\int\limits_{c=x}^{\infty}\left(\theta ^{c}\right)-al\sin \left(\alpha \right)-k\omega }{la\alpha _{x}-yb}

\alpha =j\frac{\delta \sqrt[2]{c\epsilon }}{\omega \epsilon x*\beta \sigma }/\epsilon ki_{\gamma }xx

Artikel, die hierher verlinken

Keycloak Docker und Javalin

29.05.2021

Ich wollte mich endlich mit einem der Themen beschäftigen, die bereits seit langem auf meiner Weiterbildungsliste stehen: Single Sign On und OAuth

Öffnen

GeoJson Stadtplan-Generator

10.04.2021

Ich habe mich wieder einmal mit dem Generieren von Testdaten beschäfigt - dieses Mal sollte es eine Karte eines urbanen Gebietes, sozusagen ein Stadtplan sein.

Öffnen

Vor 5 Jahren hier im Blog

Traceroute Visualisierung mittels GeoJSON

29.05.2021

Dieses Wochenende war es wieder einmal an der Zeit für ein Kaninchenbau-Projekt. Es gibt inzwischen einige kostenlose Geolocation-APIs im Netz und ich wurde - durch das Internet - auf die Idee gebracht, das Ergebnis eines Aufrufs von traceroute auf einer Landkarte zu visualisieren
Weiterlesen

Neueste Artikel

Trusted Platform Module im Thin Client Fujitsu Futro nutzen

Es geht hier speziell um das Modell s920. Bei Recherchen zu meinen letzten Experimenten hatte ich auch realisiert, dass ich einen solchen Thin Client mit montiertem TPM besitze - das musste natürlich ausprobiert werden!
Weiterlesen
Hardwarebeschleunigung zur Berechnung des Mandelbrotfraktals mittels Nvidia

Ich habe vor geraumer Zeit immer wieder einmal das Mandelbrotfraktal berechnet - auf der Kommandozeile genauso wie mittels Shadern auf der Graphikkarte. Nun bin ich dahin zurückgekehrt: Ich wollte wissen, ob dieser Code heute noch funktioniert und mit einer Nvidia-Karte ebenso funktioniert, wie damals mit meiner guten alten Radeon...
Weiterlesen
Asymmetrische Kryptographie

Ich habe mich mit der Idee schon länger getragen: Nochmal einen Rundumschlag zu asymmetrischer Kryptographie zu machen. Dabei werde ich mich auf Demonstrationen der einzelnen Konzepte und Operationen mit Beispielcode konzentrieren und zu jedem der vorgestellten Konzepte mehr oder weniger ausführlich bezüglich der Einsatzszenarien und Vor- und Nachteile Stellung beziehen
Weiterlesen

Manche nennen es Blog, manche Web-Seite - ich schreibe hier hin und wieder über meine Erlebnisse, Rückschläge und Erleuchtungen bei meinen Hobbies.

Wer daran teilhaben und eventuell sogar davon profitieren möchte, muss damit leben, daß ich hin und wieder kleine Ausflüge in Bereiche mache, die nichts mit IT, Administration oder Softwareentwicklung zu tun haben.

Ich wünsche allen Lesern viel Spaß und hin und wieder einen kleinen AHA!-Effekt...

PS: Meine öffentlichen Codeberg-Repositories findet man hier.