vorhergehender Artikel
nächster Artikel

Konstruktive Geometrie mit dem Computer

vorhergehende Artikel in: Java Komponenten
25.03.2024

Ich habe in einem vorhergehenden Artikel beschrieben, dass ich eine weitere neue Graphik-Primitive erstellt habe. Dabei musste ich mir meine verschütteten Trigonometrie-Kenntnisse wieder vor Augen führen - mit Bleistift und Papier. Das müsste doch auch anders gehen dachte ich mir und begann...

Es gibt für so etwas natürlich schon hervorragende Lösungen - ein Beispiel dafür ist GCLC - ich wollte versuchen, etwas ähnliches zu schaffen.

Mein Ansatz war, einige Methoden zur Konstruktion grundlegender geometrischer Konzepte wie Mittelsenkrechter, Winkelhalbierender,... zu schreiben, die dann mit dedizierten Methoden, die auf java.awt.Graphics2D arbeiten sollten kombiniert werden können.

Nachdem ein grundlegender Satz solcher Methoden verfügbar war, habe ich meinen Java-Editor benutzt um eine Variante eines Geometrieeditors zu schaffen, der auf jede Änderung an der Textbeschreibung (Java-Quelltext, wird mittels BeanShell interpretiert) hin die entsprechende Graphik neu zeichnet. Die Editorkomponente kann in ein separates Fenster ausgekoppelt werden - damit kann man unkompliziert mit zwei Bildschirmen arbeiten, wobei auf einem der Editor und auf dem zweiten das Vorschaubild zu sehen ist.

Fehler im Editor werden farblich hervorgehoben. Fehler sorgen nicht dafür, dass die Vorschau unbrauchbar wird - es werden alle Zeichenanweisungen bis direkt vor dem ersten Fehler ausgeführt. So bekommt man zusätzlich zu der farblichen Markierung des Fehlers im Text auch durch die Vorschau eine Ahnung dafür, wo der Fehler versteckt ist.

Die Anwendung kann die Zeichnung in verschiedenen Formaten - darunter PDF, SVG und PNG - exportieren. Natürlich funktioniert diese Methode auch nahtlos mit meiner Implementierung von Hatching oder sloppy Rendering.

Mit dem aktuellen Stand wurde zum Beispiel folgende Datei erstellt:

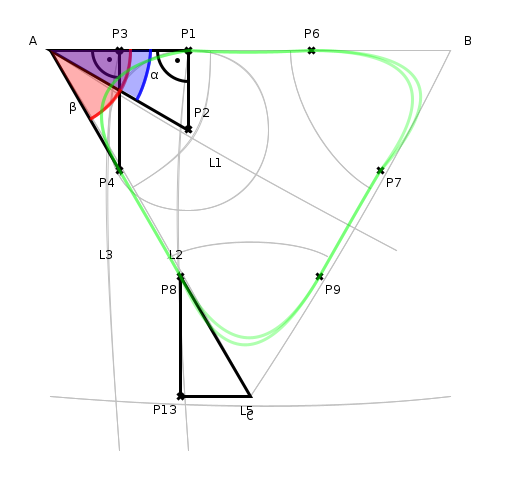Screenshot Eine Beispielkonstruktion

Der dafür nötige Text ist nachfolgend angegeben: 

import java.awt.geom.AffineTransform;
import java.awt.geom.GeneralPath;
import java.awt.geom.Line2D;
import java.awt.geom.Point2D;
import de.elbosso.ui.awt.RoughGraphics;
import java.awt.*;


double len=400;
double r=80;
double angle=60;
double halfangle=angle*0.5;
java.awt.geom.Point2D a=new Point2D.Double(0,0);
java.awt.geom.Point2D b=new Point2D.Double(1,0);
java.awt.geom.Point2D c=de.elbosso.algorithms.math2d.geometry.Utilities.unitVectorFromDirection(java.lang.Math.toRadians(angle));
java.awt.geom.Point2D d=de.elbosso.algorithms.math2d.geometry.Utilities.unitVectorFromDirection(java.lang.Math.toRadians(halfangle));
java.awt.geom.Point2D bs=de.elbosso.algorithms.math2d.geometry.Utilities.scale(b,len);
java.awt.geom.Point2D cs=de.elbosso.algorithms.math2d.geometry.Utilities.scale(c,len);
java.awt.geom.Point2D ds=de.elbosso.algorithms.math2d.geometry.Utilities.scale(d,len);
java.awt.geom.Line2D l1=new Line2D.Double(a,ds);
double ak=r/java.lang.Math.tan(java.lang.Math.toRadians(halfangle));
double gk2=ak*java.lang.Math.sin(java.lang.Math.toRadians(angle));
double ak2=ak*java.lang.Math.cos(java.lang.Math.toRadians(angle));
double gk3=ak*java.lang.Math.sin(java.lang.Math.toRadians(halfangle));
double ak3=ak*java.lang.Math.cos(java.lang.Math.toRadians(halfangle));
java.awt.geom.Point2D pak=new Point2D.Double(ak,0);
java.awt.geom.Point2D cp=new Point2D.Double(ak,len);
java.awt.geom.Line2D l2=new Line2D.Double(pak,cp);
java.awt.geom.Point2D center=de.elbosso.algorithms.math2d.geometry.Utilities.intersection(l1,l2);
java.awt.geom.Point2D p3=new Point2D.Double(gk3,0);
java.awt.geom.Point2D p4=new Point2D.Double(gk3,ak3);
java.awt.geom.Point2D p3prime=new Point2D.Double(a.getX(),p4.getY());
java.awt.geom.Point2D p5=new Point2D.Double(gk3,len);
java.awt.geom.Line2D l3=new Line2D.Double(p3,p5);
java.awt.geom.Point2D p6=new Point2D.Double(bs.getX()-pak.getX(),0);
java.awt.geom.Point2D p7=new Point2D.Double(bs.getX()-p4.getX(),p4.getY());
java.awt.geom.Point2D p8=new Point2D.Double(len/2-ak2,cs.getY()-gk2);
java.awt.geom.Point2D p9=new Point2D.Double(len/2+ak2,cs.getY()-gk2);
java.awt.geom.Point2D p10=new Point2D.Double(a.getX(),len);
java.awt.geom.Point2D p11=new Point2D.Double(a.getX(),cs.getY());
java.awt.geom.Point2D p12=new Point2D.Double(bs.getX(),cs.getY());
java.awt.geom.Line2D l4=new Line2D.Double(a,p10);
java.awt.geom.Line2D l5=new Line2D.Double(p11,p12);
java.awt.geom.Point2D p13=new Point2D.Double(p8.getX(),cs.getY());
java.awt.Graphics2D g2=new de.elbosso.algorithms.math2d.geometry.Graphics2D((java.awt.Graphics2D)g);
RoughGraphics rg=new RoughGraphics(g2,shapeCache);
rg.setSloppyness(3);
rg.setPreserveVertices(true);
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING,RenderingHints.VALUE_ANTIALIAS_ON);
g2.setBackground(Color.WHITE);
g2.setStroke(new BasicStroke(3.0f));
g2.setPaint(Color.WHITE);
//g2.fillRect(0,0,getSize().width,getSize().height);
java.awt.geom.AffineTransform at=g2.getTransform();
at.concatenate(AffineTransform.getTranslateInstance(50,50));
g2.setTransform(at);
g2.setPaint(Color.BLACK);
g2.setPaint(Color.LIGHT_GRAY);
g2.setStroke(new BasicStroke(1.0f));
de.elbosso.ui.awt.GfxUtilities.drawTriangleMarkAngles(a,cs,bs,rg);
de.elbosso.ui.awt.GfxUtilities.drawLine(l1,rg);
de.elbosso.ui.awt.GfxUtilities.drawLine(l2,rg);
de.elbosso.ui.awt.GfxUtilities.drawLine(l3,rg);
de.elbosso.ui.awt.GfxUtilities.drawLine(l5,rg);
de.elbosso.ui.awt.GfxUtilities.drawOval(new java.awt.geom.Ellipse2D.Double(center.getX()-r,center.getY()-r,r*2,r*2),rg);
g2.setStroke(new BasicStroke(3.0f));
g2.setPaint(Color.BLACK);
de.elbosso.ui.awt.GfxUtilities.drawTriangleVertices(new java.awt.geom.Point2D[]{a,bs,cs},new java.lang.String[]{"A","B","C"},rg);
de.elbosso.ui.awt.GfxUtilities.labelLine(l1,"L1",rg);
de.elbosso.ui.awt.GfxUtilities.labelLine(l2,"L2",rg);
de.elbosso.ui.awt.GfxUtilities.labelLine(l3,"L3",rg);
de.elbosso.ui.awt.GfxUtilities.labelLine(l5,"L5",rg);
de.elbosso.ui.awt.GfxUtilities.drawPoint(pak,g2,"P1", SwingConstants.NORTH);
de.elbosso.ui.awt.GfxUtilities.drawPoint(center,g2,"P2", SwingConstants.NORTH_EAST);
de.elbosso.ui.awt.GfxUtilities.drawPoint(p3,g2,"P3", SwingConstants.NORTH);
de.elbosso.ui.awt.GfxUtilities.drawPoint(p4,g2,"P4", SwingConstants.SOUTH_WEST);
de.elbosso.ui.awt.GfxUtilities.drawPoint(p6,g2,"P6", SwingConstants.NORTH);
de.elbosso.ui.awt.GfxUtilities.drawPoint(p7,g2,"P7", SwingConstants.SOUTH_EAST);
de.elbosso.ui.awt.GfxUtilities.drawPoint(p8,g2,"P8", SwingConstants.SOUTH_WEST);
de.elbosso.ui.awt.GfxUtilities.drawPoint(p9,g2,"P9", SwingConstants.SOUTH_EAST);
de.elbosso.ui.awt.GfxUtilities.drawPoint(p13,g2,"P13", SwingConstants.SOUTH_WEST);
java.awt.geom.Point2D al=de.elbosso.algorithms.math2d.geometry.Utilities.unitVectorFromDirection(java.lang.Math.toRadians(halfangle*0.5));
g2.drawString("\u03B1",(int)(al.getX()*100+2*de.elbosso.algorithms.math2d.geometry.Utilities.POINT_DIMENSION),(int)(al.getY()*100+2*de.elbosso.algorithms.math2d.geometry.Utilities.POINT_DIMENSION));
java.awt.geom.Point2D bl=de.elbosso.algorithms.math2d.geometry.Utilities.unitVectorFromDirection(java.lang.Math.toRadians(angle*1.25));
g2.drawString("\u03B2",(int)(bl.getX()*60+2*de.elbosso.algorithms.math2d.geometry.Utilities.POINT_DIMENSION),(int)(bl.getY()*60+2*de.elbosso.algorithms.math2d.geometry.Utilities.POINT_DIMENSION));
//java.awt.geom.Point2D e=intersection(new Line2D.Double(a,ds),new Line2D.Double(bs,cs));
//System.out.println(e);
//de.elbosso.algorithms.math2d.geometry.Utilities.drawPoint(e,g2,"E", SwingConstants.NORTH);
de.elbosso.ui.awt.GfxUtilities.drawTriangleMarkOnlyRightAngles(a,pak,center,g2);
de.elbosso.ui.awt.GfxUtilities.drawTriangleMarkOnlyRightAngles(a,p3,p4,g2);
de.elbosso.ui.awt.GfxUtilities.drawTriangle(p8,cs,p13,g2,false,false);
g2.setPaint(new java.awt.Color(255,0,0,80));
rg.fillArc(-80,-80,160,160,0,-(int)java.lang.Math.toDegrees(de.elbosso.algorithms.math2d.geometry.Utilities.angleOfVector(cs)));
g2.setPaint(new java.awt.Color(255,0,0,160));
rg.drawArc(-80,-80,160,160,0,-(int)java.lang.Math.toDegrees(de.elbosso.algorithms.math2d.geometry.Utilities.angleOfVector(cs)));
g2.setPaint(new java.awt.Color(0,0,255,80));
rg.fillArc(-100,-100, 200,200,0,-(int)java.lang.Math.toDegrees(de.elbosso.algorithms.math2d.geometry.Utilities.angleOfVector(ds)));
g2.setPaint(new java.awt.Color(0,0,255,160));
rg.drawArc(-100,-100, 200,200,0,-(int)java.lang.Math.toDegrees(de.elbosso.algorithms.math2d.geometry.Utilities.angleOfVector(ds)));
g2.setPaint(new java.awt.Color(0,255,0,80));
java.awt.geom.GeneralPath path=new java.awt.geom.GeneralPath();
path.moveTo(pak.getX(),pak.getY());
path.lineTo(p6.getX(),p6.getY());
path.quadTo(bs.getX(),bs.getY(),p7.getX(),p7.getY());
path.lineTo(p9.getX(),p9.getY());
path.quadTo(cs.getX(),cs.getY(),p8.getX(),p8.getY());
path.lineTo(p4.getX(),p4.getY());
path.quadTo(a.getX(),a.getY(),pak.getX(),pak.getY());
path.closePath();
rg.draw(path);

Artikel, die hierher verlinken

Processing in Java

31.01.2025

Ich habe bereits vor geraumer Zeit einen Artikel zum Thema Erzeugung von AnimGifs mittels Java veröffentlicht - hier erkläre ich nun, wie ich auf die Idee gekommen bin...

Öffnen

Alle Artikel rss Wochenübersicht Monatsübersicht Codeberg Repositories Mastodon Über mich home xmpp

Vor 5 Jahren hier im Blog

  • GeoJSON in EBMap4D

    31.07.2021

    Ich habe die Anwendung EBMap4D einer Generalüberholung unterzogen und neue Features hinzugefügt...

    Weiterlesen

Tags

AI und ML Android Basteln C und C++ Chaos Datenbanken Docker dWb+ ESP Wifi Garten Geo Go GUI Hardware Java Jupyter JupyterBinder Komponenten Links Linux Markdown Markup Music Numerik OpenSource PKI-X.509-CA Präsentationen Python QBrowser Rants Raspi Revisited Security Software-Test sQLshell TeleGrafana Verschiedenes Video Virtualisierung Windows Upcoming...

Neueste Artikel

  • Automatische Konvertierung von JavaScript nach Java

    Ich halte mich von den Themen Artificial Intelligence und Machine Learning (Large Language Models) ja fern so gut es geht - vor allem, weil ich das mal studiert habe. Manchmal überkommt mich aber die Neugierde - das Resultat war bisher immer schlechte Laune.

    Weiterlesen
  • OCR Workflow in der sQLshell

    Wie bereits in einem früheren Artikel beschrieben habe verfügt die sQLshell über eine Integration zur Erfassung von Daten aus Dokumentendirekt per Optical Character Recognition. Ich habe diese Integration weiter verfeinert und möchte hier einen exemplarischen Workflow für diese Möglichkeit zeigen

    Weiterlesen
  • Docker-Services im Homelab

    Diese Seite wird mit allen derzeit in meinem Self-Hosting Homelab betriebenen Services auf Docker-Basis befüllt (Eigenentwicklungen werden nicht genannt, sofern sie keine öffentlich verfügbaren Open-Source-Lösungen darstellen).

    Weiterlesen

Manche nennen es Blog, manche Web-Seite - ich schreibe hier hin und wieder über meine Erlebnisse, Rückschläge und Erleuchtungen bei meinen Hobbies.

Wer daran teilhaben und eventuell sogar davon profitieren möchte, muss damit leben, daß ich hin und wieder kleine Ausflüge in Bereiche mache, die nichts mit IT, Administration oder Softwareentwicklung zu tun haben.

Ich wünsche allen Lesern viel Spaß und hin und wieder einen kleinen AHA!-Effekt...

PS: Meine öffentlichen Codeberg-Repositories findet man hier.