Manchmal dauert es ein wenig länger von der Inspiration bis zur Umsetzung

Ich habe mich wieder einmal von bleeptrack inspirieren lassen: die Visualisierung von Tracks oder Trajektorien in Vektorfeldern erschien mir interessant genug, mich selbst daran auszuprobieren.

Prinzipiell funktioniert das Ganze so, dass man an einer jeden Stelle x,y einen Vektor hat mit zwei oder mehr Komponenten - eine der Komponenten ist die Komponente des Richtungsvektors in x-Richtung und eine ist die Komponente des Vektors in y-Richtung. Nun kann man die Vektoren visualisieren - nachdem man sie genormt hat sagen die Längen der kleinen Striche etwas über den Betrag des jeweiligen Vektors aus:

Beispiel eines Vektorfeldes mit 128x128 Vektoren

Diese Vektoren kann man als Ableitung einer Funktion in x- und y-Richtung betrachten. Nun kann man Trajektorien ganz ähnlich dem numerischen Lösen von Differentialgleichungssystemen einzeichnen: man nimmt die Ableitung bzw. die Richtung des Vektors als Richtung der Trajektorie an der jeweiligen x-y-Koordinate an und berechnet damit den nächsten Punkt der Trajektorie mit einer möglichst kleinen Schrittweite. An diesem Punkt bestimmt man nun wieder die Richtung des dortigen Vektors und fährt iterativ mit dem Prozess fort. Die Abbildung zeigt beispielhaft den Verlauf einiger Trajektorien, die im Mittelpunkt des Feldes beginnen, wobei jeder Startpunkt mit einem kleinen zufälligen Offset beaufschlagt wurde.

Ich habe die Vektoren aus einem Perlin-Noise-Generator gewonnen (eigentlich aus zwei solchen Generatoren - je einer für die x- und y-Komponenten des Vektors.

Interessant ist vielleicht noch, dass beim beschriebenen Verfahren die neu berechneten x,y-Koordinaten wahrscheinlich nicht auf einer der Stützstellen des Vektorfelds liegen. In einem solchen Fall kann man sich zum Beispiel damit behelfen, dass man einfach den entsprechend einer gewählten Metrik nächstliegenden Vektor benutzt. Ich bin allerdings anders vorgegangen: ich berechnete den zu benutzenden Richtungsvektor, indem ich aus den vier nächstliegenden Vektoren einen mittels komponentenweiser bilinearer Filterung erzeugte.

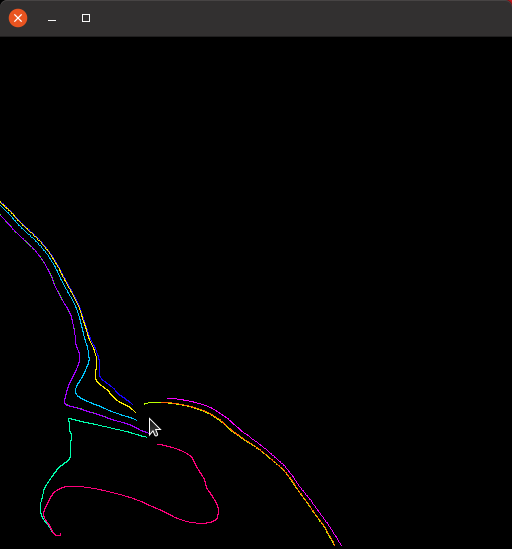
Anschließend erstellte ich eine Kompontente, die die Ergebnisse graphisch darstellt: die Position des Mauszeigers wird benutzt, um von dort ausgehend einige Trajektorien zu zeichnen, wobei der Ausgangspunkt jeder dieser Trajektorien um einen zufälligen Offset zur Position des Mauszeigers verschoben ist - hier einige Ergebnisse für unterschiedliche Positionen des Mauszeigers im oben gezeigten Vektorfeld:

Trajektorien im Vektorfeld 1

Trajektorien im Vektorfeld 2

Trajektorien im Vektorfeld 3

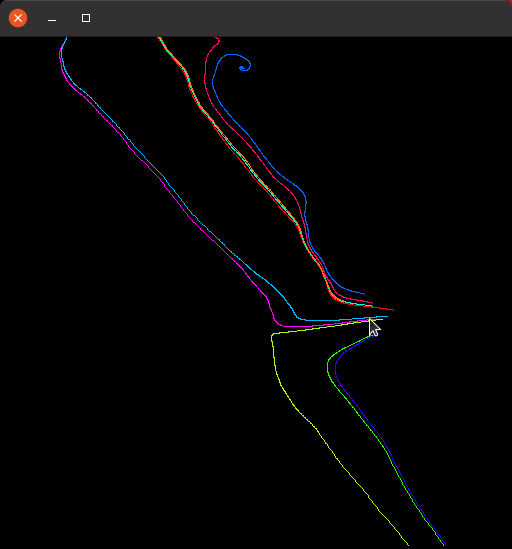Trajektorien im Vektorfeld 4