Die Apollonios-Kreisfüllung
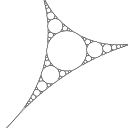
Ich habe mich wieder einmal mit dem Thema Fraktale beschäftigt - und dieses Mal ein so richtig altes dafür herausgesucht.
Dieses Fraktal ist wirklich schon sehr alt. Was ich darüber gelesen habe hat mein Interesse geweckt - aßerdem dachte ich, dass es wider einmal eine schöne Fingerübung wäre...
Nachdem ich mich ein wenig im Internet umgesehen habe bin ich beim Rosetta Code Projekt fündig geworden, das allerdings seither große Probleme zu haben scheint - der Server ist nicht mehr erreichbar - die Domain rosettacode.org kann derzeit nicht mehr aufgelöst werden
Der Code dort löst allerdings erst einmal "nur" Descartes Theorem, so dass ich noch einiges drumrum stricken musste, bis ich an einem Punkt angekommen war, an dem mein Ziel - die Erzeugung von SVG-Graphiken erreicht war:
Apollonios-Kreisfüllung als SVG mit mehr als 8000 Kreisen
Der Code dafür ist hier zu finden:
//https://rosettacode.org/wiki/Problem_of_Apollonius#Java
class Circle
{
public double[] center;
public double radius;
public Circle(double[] center, double radius)
{
this.center = center;
this.radius = radius;
}
public Circle(java.awt.geom.Ellipse2D ell)
{
if(ell.getWidth()!=ell.getHeight())
throw new java.lang.IllegalArgumentException("only circles allowed - no ellipses!");
this.center=new double[2];
this.radius=ell.getWidth()*0.5;
this.center[0]=ell.getCenterX();
this.center[1]=ell.getCenterY();
}
public String toString()
{
return String.format("Circle[x=%.2f,y=%.2f,r=%.2f]", center[0], center[1], radius);
}
public java.lang.String toSvg(double strokeWidth)
{
return "<circle cx=\""+center[0]+"\" cy=\""+center[1]+"\" r=\""+radius+"\" stroke=\"black\" stroke-width=\""+(strokeWidth<radius*0.33?strokeWidth:radius*0.33)+"\" fill=\"none\"/>";
}
public boolean isValid()
{
return (((center!=null)&&(java.lang.Double.isNaN(radius)==false))&&((java.lang.Double.isNaN(center[0])==false)&&(java.lang.Double.isNaN(center[1])==false)));
}
public double getRadius()
{
return radius;
}
public java.awt.geom.Point2D getCenter()
{
return new java.awt.geom.Point2D.Double(center[0],center[1]);
}
public boolean contains(Circle other)
{
return getCenter().distance(other.getCenter())+other.getRadius()<getRadius()+0.00005;
}
}
public class ApolloniusSolver
{
/**
* Solves the Problem of Apollonius (finding a circle tangent to three other circles in the plane).
* The method uses approximately 68 heavy operations (multiplication, division, square-roots).
*
* @param c1 One of the circles in the problem
* @param c2 One of the circles in the problem
* @param c3 One of the circles in the problem
* @param s1 An indication if the solution should be externally or internally tangent (+1/-1) to c1
* @param s2 An indication if the solution should be externally or internally tangent (+1/-1) to c2
* @param s3 An indication if the solution should be externally or internally tangent (+1/-1) to c3
* @return The circle that is tangent to c1, c2 and c3.
*/
public static Circle solveApollonius(Circle c1, Circle c2, Circle c3, int s1, int s2, int s3)
{
double x1 = c1.center[0];
double y1 = c1.center[1];
double r1 = c1.radius;
double x2 = c2.center[0];
double y2 = c2.center[1];
double r2 = c2.radius;
double x3 = c3.center[0];
double y3 = c3.center[1];
double r3 = c3.radius;
// Currently optimized for fewest multiplications. Should be optimized for
// readability
double v11 = 2 * x2 - 2 * x1;
double v12 = 2 * y2 - 2 * y1;
double v13 = x1 * x1 - x2 * x2 + y1 * y1 - y2 * y2 - r1 * r1 + r2 * r2;
double v14 = 2 * s2 * r2 - 2 * s1 * r1;
double v21 = 2 * x3 - 2 * x2;
double v22 = 2 * y3 - 2 * y2;
double v23 = x2 * x2 - x3 * x3 + y2 * y2 - y3 * y3 - r2 * r2 + r3 * r3;
double v24 = 2 * s3 * r3 - 2 * s2 * r2;
double w12 = v12 / v11;
double w13 = v13 / v11;
double w14 = v14 / v11;
double w22 = v22 / v21 - w12;
double w23 = v23 / v21 - w13;
double w24 = v24 / v21 - w14;
double P = -w23 / w22;
double Q = w24 / w22;
double M = -w12 * P - w13;
double N = w14 - w12 * Q;
double a = N * N + Q * Q - 1;
double b = 2 * M * N - 2 * N * x1 + 2 * P * Q - 2 * Q * y1 + 2 * s1 * r1;
double c = x1 * x1 + M * M - 2 * M * x1 + P * P + y1 * y1 - 2 * P * y1 - r1 * r1;
// Find a root of a quadratic equation. This requires the circle centers not
// to be e.g. colinear
double D = b * b - 4 * a * c;
double rs = (-b - Math.sqrt(D)) / (2 * a);
double xs = M + N * rs;
double ys = P + Q * rs;
return new Circle(new double[]
{xs, ys}, rs);
}
public static void main(final String[] args)throws java.io.FileNotFoundException
{
Circle c1 = new Circle(new double[]
{0, 0}, 1);
Circle c2 = new Circle(new double[]
{4, 0}, 1);
Circle c3 = new Circle(new double[]
{2, 4}, 2);
java.awt.geom.Point2D a=new java.awt.geom.Point2D.Double(310,410);
java.awt.geom.Point2D b=new java.awt.geom.Point2D.Double(600,410);
java.awt.geom.Point2D c=new java.awt.geom.Point2D.Double(400,590);
de.elbosso.algorithms.math2d.geometry.Triangle2D t=new de.elbosso.algorithms.math2d.geometry.Triangle2D(a,b,c);
java.awt.geom.Ellipse2D[] anKreise=t.getExternallyTangentCircles();
c1=new Circle(anKreise[0]);
c2=new Circle(anKreise[1]);
c3=new Circle(anKreise[2]);
java.util.List<Circle> circles=new java.util.LinkedList();
circles.add(c1);
circles.add(c2);
circles.add(c3);
Circle outer=solveApollonius(c1, c2, c3, 1, 1, 1);
circles.add(outer);
addCircles(c1,c2,outer,circles);
addCircles(c1,c3,outer,circles);
addCircles(c3,c2,outer,circles);
addCircles(c1,c2,c3,circles);
java.lang.StringBuffer buf=new java.lang.StringBuffer();
buf.append("<svg xmlns=\"http://www.w3.org/2000/svg\" version=\"1.1\" width=\""+outer.getRadius()*3+"\" height=\""+outer.getRadius()*3+"\">");
for(Circle circle:circles)
{
buf.append(circle.toSvg(0.2));
buf.append("\n");
}
buf.append("</svg>");
java.io.File f=new java.io.File("/tmp/theFile.svg");
java.io.PrintWriter pw=new java.io.PrintWriter(f);
pw.println(buf.toString());
pw.flush();
pw.close();
}
private static void addCircles(Circle c1,Circle c2, Circle c3, java.util.List<Circle> circles)
{
int s1=-1;
int s2=-1;
int s3=-1;
if((c1.contains(c2))||(c1.contains(c3)))
s1=1;
if((c2.contains(c1))||(c2.contains(c3)))
s2=1;
if((c3.contains(c2))||(c3.contains(c1)))
s3=1;
java.util.List<Circle> resultsFromThisIteration=new java.util.LinkedList();
Circle c=solveApollonius(c1,c2,c3,s1,s2,s3);
if(c.isValid())
resultsFromThisIteration.add(c);
circles.addAll(resultsFromThisIteration);
if((resultsFromThisIteration.isEmpty()==false)&&(resultsFromThisIteration.get(0).getRadius()>0.5))
{
addCircles(c1,c2,resultsFromThisIteration.get(0),circles);
addCircles(c1,c3,resultsFromThisIteration.get(0),circles);
addCircles(c3,c2,resultsFromThisIteration.get(0),circles);
}
}
}
Es ist schwierig, die graphische Representation ansprechend zu gestalten, da man die Dicke der Strichstärke eigentlich abhängig vom Radius des jeweiligen Kreises variieren müsste - und selbst das sorgt nur für mittelmäßig gute Resultate - wenn man in das oben abgebildete SVG hineinzoomt wird man feststellen, dass Stellen in denen sich Kreise mit relativ großem und relativ kleinem Radius berühren nicht "schön" dargestellt werden. Man bräuchte etwas wie Metafonts Konzept einer Strichstärke, die unabhängig von Zoomstufe und Auflösung des Zielmediums jeweils exakt einen Pixel breit ist.
So etwas existiert dankenswerterweise in SVG: "non-scaling-stroke" - damit ist exakt das möglich. Eine Variante der oben bereits gezeigten Graphik mit dieser Methode ist hier unten angehängt - nicht alle Browser unterstützen dieses Attribut. Man kann aber die Auswirkungen zum Beispiel ganz hervorragend in Inkscape betrachten.
Apollonios-Kreisfüllung als SVG mit mehr als 8000 Kreisen und zoomunabhängiger Strichstärke von 1 Pixel
Vor 5 Jahren hier im Blog
-
Storage Server Konfiguration I
31.01.2021
Ich habe zu Weiterbildungszwecken aus alten PC-Komponenten ein Serversystem zusammengebaut und stelle hier die Konfiguration als Storage-Server vor
Weiterlesen
Tags
Android Basteln C und C++ Chaos Datenbanken Docker dWb+ ESP Wifi Garten Geo Go GUI Gui Hardware Hardware. Links Java Java. Komponenten Jupyter JupyterBinder Komponenten Links Linuc Linux Markdown Markup Music Numerik OpenSource PKI-X.509-CA Präsentationen Python QBrowser Rants Raspi Revisited Security Software-Test sQLshell TeleGrafana Verschiedenes Video Virtualisierung Windows Upcoming...
Neueste Artikel
-
 Asymmetrische Kryptographie
Asymmetrische Kryptographie
Ich habe mich mit der Idee schon länger getragen: Nochmal einen Rundumschlag zu asymmetrischer Kryptographie zu machen. Dabei werde ich mich auf Demonstrationen der einzelnen Konzepte und Operationen mit Beispielcode konzentrieren und zu jedem der vorgestellten Konzepte mehr oder weniger ausführlich bezüglich der Einsatzszenarien und Vor- und Nachteile Stellung beziehen
Weiterlesen -
LinkCollections 2026 I
Nach der letzten losen Zusammenstellung (für mich) interessanter Links aus den Tiefen des Internet von 2025 folgt hier gleich die erste für dieses Jahr:
Weiterlesen -
AtTiny85 zur Ansteuerung von OLED-Infodisplays via USB
Ich hatte neulich bemerkt, dass ich bei meinem Wechsel von Github zu Codeberg nicht alle meine Repositories erwischt hatte...
Weiterlesen
Manche nennen es Blog, manche Web-Seite - ich schreibe hier hin und wieder über meine Erlebnisse, Rückschläge und Erleuchtungen bei meinen Hobbies.
Wer daran teilhaben und eventuell sogar davon profitieren möchte, muss damit leben, daß ich hin und wieder kleine Ausflüge in Bereiche mache, die nichts mit IT, Administration oder Softwareentwicklung zu tun haben.
Ich wünsche allen Lesern viel Spaß und hin und wieder einen kleinen AHA!-Effekt...
PS: Meine öffentlichen Codeberg-Repositories findet man hier.





